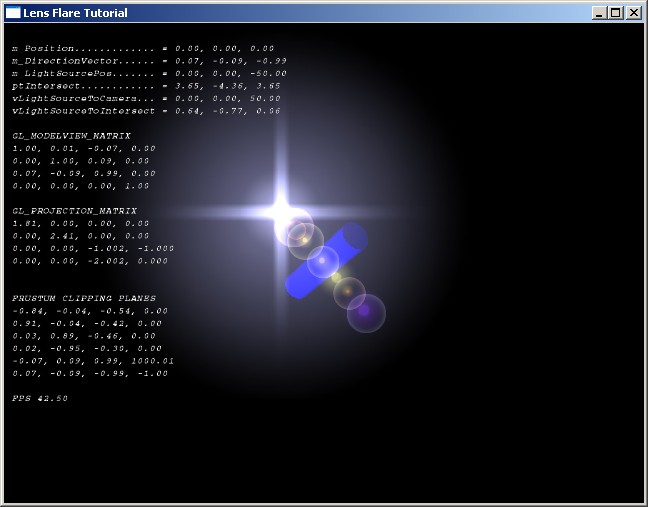
Lekce 44 - Čočkové efekty
Čočkové efekty vznikají po dopadu paprsku světla např. na objektiv kamery nebo fotoaparátu. Podíváte-li se na záři vyvolanou čočkou, zjistíte, že jednotlivé útvary mají jednu společnou věc. Pozorovateli se zdá, jako by se všechny pohybovaly skrz střed scény. S tímto na mysli můžeme osu z jednoduše odstranit a vytvářet vše ve 2D. Jediný problém související s nepřítomností z souřadnice je, jak zjistit, jestli se zdroj světla nachází ve výhledu kamery nebo ne. Připravte se proto na trochu matematiky.
Ahoj všichni, jsem tu s dalším tutoriálem. Rozšíříme naši třídu glCamera o čočkové efekty (Překl.: v originále Lens Flare - čočková záře), které jsou sice náročné na množství výpočtů, ale vypadají opravdu realisticky. Jak už jsem napsal, do třídy kamery přidáme možnost, jak zjistit, jestli se bod nebo koule nachází ve výhledu kamery na scénu. Neměli bychom však při tom odrovnat procesor.
Jsem na rozpacích, ale musím zmínit, že třída kamery obsahuje chybu. Před tím, než začneme, musíme ji záplatovat. Funkci SetPerspective() upravte podle následujícího vzoru.
void glCamera::SetPerspective()
{
GLfloat Matrix[16];// Pole pro modelview matici
glVector v;// Směr a rychlost kamery
glRotatef(m_HeadingDegrees, 0.0f, 1.0f, 0.0f);// Výpočet směrového vektoru
glRotatef(m_PitchDegrees, 1.0f, 0.0f, 0.0f);
glGetFloatv(GL_MODELVIEW_MATRIX, Matrix);// Získání matice
m_DirectionVector.i = Matrix[8];// Směrový vektor
m_DirectionVector.j = Matrix[9];
m_DirectionVector.k = -Matrix[10];// Musí být invertován
glLoadIdentity();// Reset matice
glRotatef(m_PitchDegrees, 1.0f, 0.0f, 0.0f);// Správná orientace scény
glRotatef(m_HeadingDegrees, 0.0f, 1.0f, 0.0f);
v = m_DirectionVector;// Aktualizovat směr podle rychlosti
v *= m_ForwardVelocity;
m_Position.x += v.i;// Inkrementace pozice vektorem
m_Position.y += v.j;
m_Position.z += v.k;
glTranslatef(-m_Position.x, -m_Position.y, -m_Position.z);// Přesun na novou pozici
}
Před tím, než se pustíme do kódování, si nakreslíme čtyři textury pro čočkovou záři. První představuje mlhavou záři nebo sálání a bude vždy umisťována na pozici světelného zdroje. Pomocí další můžeme vytvářet záblesky zářící ven ze světla. Opět ji umístíme na jeho pozici. Třetí se vzhledem podobá první textuře, ale uprostřed je mnohem více definovaná. Budeme jí dynamicky pohybovat přes scénu. Poslední textura je zářící, dutě vypadající kruh, který budeme přesunovat v závislosti na pozici a orientaci kamery. Existují samozřejmě i další typy textur; pro další informace se podívejte na reference uvedené na konci tutoriálu.




Teď byste už měli mít alespoň představu, co budeme vykreslovat. Obecně se dá říci, že se čočkový efekt nikdy neobjeví, dokud se nepodíváme do zdroje světla nebo alespoň jeho směrem, a proto potřebujeme najít cestu, jak zjistit, jestli se daný bod (pozice světla) nachází ve výhledu kamery nebo ne. Můžeme vynásobit modelview a projekční matici a potom nalézt ořezávací roviny, které OpenGL používá. Druhá možnost je použít rozšíření GL_HP_occlusion_test nebo GL_NV_occlusion_query, ale ne každá grafická karta je implementuje. My použijeme věc, která funguje vždy a všude - matematiku.
Překl.: Občas, když je něco málo vysvětlené, přidávám vlastní texty, ale teď to po mně prosím nechtějte :-)
void glCamera::UpdateFrustum()// Získání ořezávacích rovin
{
GLfloat clip[16];// Pomocná matice
GLfloat proj[16];// Projekční matice
GLfloat modl[16];// Modelview matice
GLfloat t;// Pomocná
glGetFloatv(GL_PROJECTION_MATRIX, proj);// Získání projekční matice
glGetFloatv(GL_MODELVIEW_MATRIX, modl);// Získání modelview matice
// Vynásobí projekční matici pomocí modelview
clip[ 0] = modl[ 0] * proj[ 0] + modl[ 1] * proj[ 4] + modl[ 2] * proj[ 8] + modl[ 3] * proj[12];
clip[ 1] = modl[ 0] * proj[ 1] + modl[ 1] * proj[ 5] + modl[ 2] * proj[ 9] + modl[ 3] * proj[13];
clip[ 2] = modl[ 0] * proj[ 2] + modl[ 1] * proj[ 6] + modl[ 2] * proj[10] + modl[ 3] * proj[14];
clip[ 3] = modl[ 0] * proj[ 3] + modl[ 1] * proj[ 7] + modl[ 2] * proj[11] + modl[ 3] * proj[15];
clip[ 4] = modl[ 4] * proj[ 0] + modl[ 5] * proj[ 4] + modl[ 6] * proj[ 8] + modl[ 7] * proj[12];
clip[ 5] = modl[ 4] * proj[ 1] + modl[ 5] * proj[ 5] + modl[ 6] * proj[ 9] + modl[ 7] * proj[13];
clip[ 6] = modl[ 4] * proj[ 2] + modl[ 5] * proj[ 6] + modl[ 6] * proj[10] + modl[ 7] * proj[14];
clip[ 7] = modl[ 4] * proj[ 3] + modl[ 5] * proj[ 7] + modl[ 6] * proj[11] + modl[ 7] * proj[15];
clip[ 8] = modl[ 8] * proj[ 0] + modl[ 9] * proj[ 4] + modl[10] * proj[ 8] + modl[11] * proj[12];
clip[ 9] = modl[ 8] * proj[ 1] + modl[ 9] * proj[ 5] + modl[10] * proj[ 9] + modl[11] * proj[13];
clip[10] = modl[ 8] * proj[ 2] + modl[ 9] * proj[ 6] + modl[10] * proj[10] + modl[11] * proj[14];
clip[11] = modl[ 8] * proj[ 3] + modl[ 9] * proj[ 7] + modl[10] * proj[11] + modl[11] * proj[15];
clip[12] = modl[12] * proj[ 0] + modl[13] * proj[ 4] + modl[14] * proj[ 8] + modl[15] * proj[12];
clip[13] = modl[12] * proj[ 1] + modl[13] * proj[ 5] + modl[14] * proj[ 9] + modl[15] * proj[13];
clip[14] = modl[12] * proj[ 2] + modl[13] * proj[ 6] + modl[14] * proj[10] + modl[15] * proj[14];
clip[15] = modl[12] * proj[ 3] + modl[13] * proj[ 7] + modl[14] * proj[11] + modl[15] * proj[15];
m_Frustum[0][0] = clip[ 3] - clip[ 0];// Získání pravé roviny
m_Frustum[0][1] = clip[ 7] - clip[ 4];
m_Frustum[0][2] = clip[11] - clip[ 8];
m_Frustum[0][3] = clip[15] - clip[12];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[0][0] * m_Frustum[0][0] + m_Frustum[0][1] * m_Frustum[0][1] + m_Frustum[0][2] * m_Frustum[0][2] ));
m_Frustum[0][0] /= t;
m_Frustum[0][1] /= t;
m_Frustum[0][2] /= t;
m_Frustum[0][3] /= t;
m_Frustum[1][0] = clip[ 3] + clip[ 0];// Získání levé roviny
m_Frustum[1][1] = clip[ 7] + clip[ 4];
m_Frustum[1][2] = clip[11] + clip[ 8];
m_Frustum[1][3] = clip[15] + clip[12];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[1][0] * m_Frustum[1][0] + m_Frustum[1][1] * m_Frustum[1][1] + m_Frustum[1][2] * m_Frustum[1][2] ));
m_Frustum[1][0] /= t;
m_Frustum[1][1] /= t;
m_Frustum[1][2] /= t;
m_Frustum[1][3] /= t;
m_Frustum[2][0] = clip[ 3] + clip[ 1];// Získání dolní roviny
m_Frustum[2][1] = clip[ 7] + clip[ 5];
m_Frustum[2][2] = clip[11] + clip[ 9];
m_Frustum[2][3] = clip[15] + clip[13];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[2][0] * m_Frustum[2][0] + m_Frustum[2][1] * m_Frustum[2][1] + m_Frustum[2][2] * m_Frustum[2][2] ));
m_Frustum[2][0] /= t;
m_Frustum[2][1] /= t;
m_Frustum[2][2] /= t;
m_Frustum[2][3] /= t;
m_Frustum[3][0] = clip[ 3] - clip[ 1];// Získání horní roviny
m_Frustum[3][1] = clip[ 7] - clip[ 5];
m_Frustum[3][2] = clip[11] - clip[ 9];
m_Frustum[3][3] = clip[15] - clip[13];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[3][0] * m_Frustum[3][0] + m_Frustum[3][1] * m_Frustum[3][1] + m_Frustum[3][2] * m_Frustum[3][2] ));
m_Frustum[3][0] /= t;
m_Frustum[3][1] /= t;
m_Frustum[3][2] /= t;
m_Frustum[3][3] /= t;
m_Frustum[4][0] = clip[ 3] - clip[ 2];// Získání zadní roviny
m_Frustum[4][1] = clip[ 7] - clip[ 6];
m_Frustum[4][2] = clip[11] - clip[10];
m_Frustum[4][3] = clip[15] - clip[14];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[4][0] * m_Frustum[4][0] + m_Frustum[4][1] * m_Frustum[4][1] + m_Frustum[4][2] * m_Frustum[4][2] ));
m_Frustum[4][0] /= t;
m_Frustum[4][1] /= t;
m_Frustum[4][2] /= t;
m_Frustum[4][3] /= t;
m_Frustum[5][0] = clip[ 3] + clip[ 2];// Získání přední roviny
m_Frustum[5][1] = clip[ 7] + clip[ 6];
m_Frustum[5][2] = clip[11] + clip[10];
m_Frustum[5][3] = clip[15] + clip[14];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[5][0] * m_Frustum[5][0] + m_Frustum[5][1] * m_Frustum[5][1] + m_Frustum[5][2] * m_Frustum[5][2] ));
m_Frustum[5][0] /= t;
m_Frustum[5][1] /= t;
m_Frustum[5][2] /= t;
m_Frustum[5][3] /= t;
}
Tato funkce byla opravdu náročná! Jsem si jistý, že už víte, proč vznikají nejrůznější OpenGL rozšíření. Ačkoli je matematika celkem přímočará, její strašná délka zobrazuje věci složitě. Použili jsme celkem 190 základních operací (násobení, dělení, sčítání, odčítání), plus šest druhých odmocnin. Protože ji budeme volat při každém překreslení scény, mohla by se snaha o optimalizaci vyplatit. Dokud nemodifikujeme projekční matici translací nebo rotací, můžeme používat její rychlejší ekvivalent UpdateFrustumFaster().
void glCamera::UpdateFrustumFaster()// Získání ořezávacích rovin (optimalizovaná funkce)
{
GLfloat clip[16];// Pomocná matice
GLfloat proj[16];// Projekční matice
GLfloat modl[16];// Modelview matice
GLfloat t;// Pomocná
glGetFloatv(GL_PROJECTION_MATRIX, proj);// Získání projekční matice
glGetFloatv(GL_MODELVIEW_MATRIX, modl);// Získání modelview matice
// Vynásobí projekční matici pomocí modelview (nesmí být před tím použita rotace ani translace)
clip[ 0] = modl[ 0] * proj[ 0];
clip[ 1] = modl[ 1] * proj[ 5];
clip[ 2] = modl[ 2] * proj[10] + modl[ 3] * proj[14];
clip[ 3] = modl[ 2] * proj[11];
clip[ 4] = modl[ 4] * proj[ 0];
clip[ 5] = modl[ 5] * proj[ 5];
clip[ 6] = modl[ 6] * proj[10] + modl[ 7] * proj[14];
clip[ 7] = modl[ 6] * proj[11];
clip[ 8] = modl[ 8] * proj[ 0];
clip[ 9] = modl[ 9] * proj[ 5];
clip[10] = modl[10] * proj[10] + modl[11] * proj[14];
clip[11] = modl[10] * proj[11];
clip[12] = modl[12] * proj[ 0];
clip[13] = modl[13] * proj[ 5];
clip[14] = modl[14] * proj[10] + modl[15] * proj[14];
clip[15] = modl[14] * proj[11];
m_Frustum[0][0] = clip[ 3] - clip[ 0];// Získání pravé roviny
m_Frustum[0][1] = clip[ 7] - clip[ 4];
m_Frustum[0][2] = clip[11] - clip[ 8];
m_Frustum[0][3] = clip[15] - clip[12];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[0][0] * m_Frustum[0][0] + m_Frustum[0][1] * m_Frustum[0][1] + m_Frustum[0][2] * m_Frustum[0][2] ));
m_Frustum[0][0] /= t;
m_Frustum[0][1] /= t;
m_Frustum[0][2] /= t;
m_Frustum[0][3] /= t;
m_Frustum[1][0] = clip[ 3] + clip[ 0];// Získání levé roviny
m_Frustum[1][1] = clip[ 7] + clip[ 4];
m_Frustum[1][2] = clip[11] + clip[ 8];
m_Frustum[1][3] = clip[15] + clip[12];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[1][0] * m_Frustum[1][0] + m_Frustum[1][1] * m_Frustum[1][1] + m_Frustum[1][2] * m_Frustum[1][2] ));
m_Frustum[1][0] /= t;
m_Frustum[1][1] /= t;
m_Frustum[1][2] /= t;
m_Frustum[1][3] /= t;
m_Frustum[2][0] = clip[ 3] + clip[ 1];// Získání spodní roviny
m_Frustum[2][1] = clip[ 7] + clip[ 5];
m_Frustum[2][2] = clip[11] + clip[ 9];
m_Frustum[2][3] = clip[15] + clip[13];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[2][0] * m_Frustum[2][0] + m_Frustum[2][1] * m_Frustum[2][1] + m_Frustum[2][2] * m_Frustum[2][2] ));
m_Frustum[2][0] /= t;
m_Frustum[2][1] /= t;
m_Frustum[2][2] /= t;
m_Frustum[2][3] /= t;
m_Frustum[3][0] = clip[ 3] - clip[ 1];// Získání horní roviny
m_Frustum[3][1] = clip[ 7] - clip[ 5];
m_Frustum[3][2] = clip[11] - clip[ 9];
m_Frustum[3][3] = clip[15] - clip[13];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[3][0] * m_Frustum[3][0] + m_Frustum[3][1] * m_Frustum[3][1] + m_Frustum[3][2] * m_Frustum[3][2] ));
m_Frustum[3][0] /= t;
m_Frustum[3][1] /= t;
m_Frustum[3][2] /= t;
m_Frustum[3][3] /= t;
m_Frustum[4][0] = clip[ 3] - clip[ 2];// Získání zadní roviny
m_Frustum[4][1] = clip[ 7] - clip[ 6];
m_Frustum[4][2] = clip[11] - clip[10];
m_Frustum[4][3] = clip[15] - clip[14];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[4][0] * m_Frustum[4][0] + m_Frustum[4][1] * m_Frustum[4][1] + m_Frustum[4][2] * m_Frustum[4][2] ));
m_Frustum[4][0] /= t;
m_Frustum[4][1] /= t;
m_Frustum[4][2] /= t;
m_Frustum[4][3] /= t;
m_Frustum[5][0] = clip[ 3] + clip[ 2];// Získání přední roviny
m_Frustum[5][1] = clip[ 7] + clip[ 6];
m_Frustum[5][2] = clip[11] + clip[10];
m_Frustum[5][3] = clip[15] + clip[14];
// Normalizace výsledku
t = GLfloat(sqrt( m_Frustum[5][0] * m_Frustum[5][0] + m_Frustum[5][1] * m_Frustum[5][1] + m_Frustum[5][2] * m_Frustum[5][2] ));
m_Frustum[5][0] /= t;
m_Frustum[5][1] /= t;
m_Frustum[5][2] /= t;
m_Frustum[5][3] /= t;
}
Operací se provádí stále mnoho, ale oproti předchozí verzi, je jich pouze něco přes polovinu (102). Optimalizace byla celkem jednoduchá, odstranil jsem pouze všechna násobení, která se díky nule vykrátí. Pokud chcete kompletní optimalizaci, použijte již zmíněná rozšíření, která za vás udělají stejnou práci a navíc mnohem rychleji, protože všechny výpočty proběhnou na hardwaru grafické karty. Ačkoli volání obou UpdateFrustum() funkcí navyšuje výkonnostní ztrátu, můžeme nyní snadno zjistit, jestli se libovolný bod nachází ve výhledu kamery. Obsahuje-li scéna více objektů náročných na rendering, bude určitě výhodné vykreslovat pouze ty, které půjdou vidět - například u rozsáhlého terénu.
PointInFrustum() vrácením true oznámí, že se bod předaný v parametru nachází ve viditelné oblasti okna. Druhá funkce je prakticky stejná, ale jedná se o kouli.
BOOL glCamera::PointInFrustum(glPoint p)// Bude bod vidět na scéně?
{
int i;
for(i = 0; i < 6; i++)// Bod se musí nacházet mezi všemi šesti ořezávacími rovinami
{
if(m_Frustum[i][0] * p.x + m_Frustum[i][1] * p.y + m_Frustum[i][2] * p.z + m_Frustum[i][3] <= 0)
{
return FALSE;
}
}
return TRUE;
}
BOOL glCamera::SphereInFrustum(glPoint p, GLfloat Radius)// Bude koule vidět na scéně?
{
int i;
for(i = 0; i < 6; i++)// Koule se musí nacházet mezi všemi šesti ořezávacími rovinami
{
if(m_Frustum[i][0] * p.x + m_Frustum[i][1] * p.y + m_Frustum[i][2] * p.z + m_Frustum[i][3] <= -Radius)
{
return FALSE;
}
}
return TRUE;
}
Ve funkci IsOccluded() požádáme gluProject() o zjištění, do které části viewportu bude zadaný bod projektován. Pozice ve viewportu odpovídá souřadnicím v depth bufferu. Pokud bude hloubka pixelu v bufferu menší než hloubka našeho bodu, je jasné, že se už něco nachází před ním.
bool glCamera::IsOccluded(glPoint p)// Je před bodem něco vykresleno?
{
GLint viewport[4];// Data viewportu
GLdouble mvmatrix[16], projmatrix[16];// Transformační matice
GLdouble winx, winy, winz;// Výsledné souřadnice
GLdouble flareZ;// Hloubka záře v obrazovce
GLfloat bufferZ;// Hloubka z bufferu
glGetIntegerv(GL_VIEWPORT, viewport);// Získání viewportu
glGetDoublev(GL_MODELVIEW_MATRIX, mvmatrix);// Získání modelview matice
glGetDoublev(GL_PROJECTION_MATRIX, projmatrix);// Získání projekční matice
// Kam do viewportu (2D) se vykreslí bod (3D)
gluProject(p.x, p.y, p.z, mvmatrix, projmatrix, viewport, &winx, &winy, &winz);
flareZ = winz;
glReadPixels(winx, winy, 1, 1, GL_DEPTH_COMPONENT, GL_FLOAT, &bufferZ);// Hloubka v depth bufferu
if (bufferZ < flareZ)// Před bodem se nachází objekt
{
return true;
}
else// Nic před bodem není
{
return false;
}
}
Všechny obdélníky objektů čočkového efektu by měly být vykreslovány na rovinu rovnoběžnou s obrazovkou monitoru, ale může se stát, že budou kvůli rotacím nakloněné. To je problém, protože by se měly zobrazit ploché i v případě, že se díváme na zdroj světla ze strany. Namísto otexturovaného quadu bychom mohli s výhodou využít point sprity. Když chceme nakreslit "klasický" obdélník, předáme OpenGL souřadnice čtyř bodů, texturovací koordináty a normálové vektory. Na rozdíl od toho point sprite vyžaduje pouze x, y, z souřadnice a nic jiného. Grafická karta vykreslí kolem těchto souřadnic obdélník, který bude vždy orientován k obrazovce. Možná se vám při programování částicových systémů stalo, že po natočení scény o 90 stupňů všechny částice zmizely, protože byly vykreslovány kolmo k ploše obrazovky. Právě pro ně se hodí point sprity nejvíce, ale pro čočkové efekty také. Jejich velká nevýhoda spočívá v implementaci, existují pouze jako rozšíření (GL_NV_point_sprite), takže se může stát, že je grafická karta nebude podporovat. Ani zde tedy rozšíření nepoužijeme. Řešení může spočívat v invertování všech rotací, nicméně problémy nastanou, pokud se kamera dostane za zdroj světla. Proto, abychom tomu předešli, budeme při pohybu kamerou zároveň měnit také polohu světla. Získáme i vedlejší efekt, zdroj světla se bude jevit jakoby stále ve stejné vzdálenosti a také dovolí čočkovým efektům o trochu vylepšit pohybování po přímé lince.
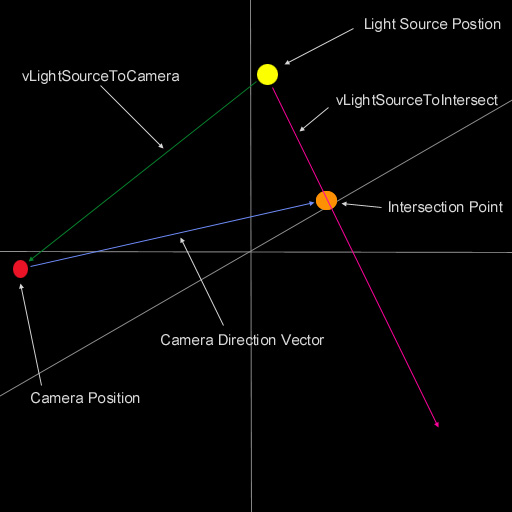
Vypočteme vzdálenost kamery od světla a přes směrový vektor kamery získáme průsečík, jehož vzdálenost od kamery musí být stejná jako vzdálenost kamery a světla. Máme-li průsečík, můžeme nalézt vektor, přes který vykreslíme všechny části čočkového efektu. Obrázek bude možná názornější...
void glCamera::RenderLensFlare()// Vykreslení čočkových objektů
{
GLfloat Length = 0.0f;
if(SphereInFrustum(m_LightSourcePos, 1.0f) == TRUE)// Pouze pokud kamera směřuje ke světlu
{
vLightSourceToCamera = m_Position - m_LightSourcePos;// Vektor od kamery ke světlu
Length = vLightSourceToCamera.Magnitude();// Vzdálenost kamery od světla
ptIntersect = m_DirectionVector * Length;// Bod průsečíku
ptIntersect += m_Position;
vLightSourceToIntersect = ptIntersect - m_LightSourcePos;// Vektor mezi světlem a průsečíkem
Length = vLightSourceToIntersect.Magnitude();// Vzdálenost světla a průsečíku
vLightSourceToIntersect.Normalize();// Normalizace vektoru
Na získaném směrovém vektoru vykreslíme záblesky. Posuneme se o x jednotek dolů po vektoru vLightSourceToIntersect a následným přičtením k pozici světla získáme nový požadovaný bod.
// Nastavení OpenGL
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE);
glDisable(GL_DEPTH_TEST);
glEnable(GL_TEXTURE_2D);
if (!IsOccluded(m_LightSourcePos))// Před středem záře nesmí být žádný objekt
{
// Vykreslení záře
RenderBigGlow(0.60f, 0.60f, 0.8f, 1.0f, m_LightSourcePos, 16.0f);
RenderStreaks(0.60f, 0.60f, 0.8f, 1.0f, m_LightSourcePos, 16.0f);
RenderGlow(0.8f, 0.8f, 1.0f, 0.5f, m_LightSourcePos, 3.5f);
pt = vLightSourceToIntersect * (Length * 0.1f);// Bod ve 20% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderGlow(0.9f, 0.6f, 0.4f, 0.5f, pt, 0.6f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.15f);// Bod ve 30% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderHalo(0.8f, 0.5f, 0.6f, 0.5f, pt, 1.7f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.175f);// Bod ve 35% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderHalo(0.9f, 0.2f, 0.1f, 0.5f, pt, 0.83f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.285f);// Bod ve 57% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderHalo(0.7f, 0.7f, 0.4f, 0.5f, pt, 1.6f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.2755f);// Bod ve 55.1% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderGlow(0.9f, 0.9f, 0.2f, 0.5f, pt, 0.8f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.4775f);// Bod ve 95.5% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderGlow(0.93f, 0.82f, 0.73f, 0.5f, pt, 1.0f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.49f);// Bod ve 98% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderHalo(0.7f, 0.6f, 0.5f, 0.5f, pt, 1.4f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.65f);// Bod ve 130% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderGlow(0.7f, 0.8f, 0.3f, 0.5f, pt, 1.8f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.63f);// Bod ve 126% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderGlow(0.4f, 0.3f, 0.2f, 0.5f, pt, 1.4f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.8f);// Bod ve 160% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderHalo(0.7f, 0.5f, 0.5f, 0.5f, pt, 1.4f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.7825f);// Bod ve 156.5% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderGlow(0.8f, 0.5f, 0.1f, 0.5f, pt, 0.6f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 1.0f);// Bod ve 200% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderHalo(0.5f, 0.5f, 0.7f, 0.5f, pt, 1.7f);// Vykreslení záře
pt = vLightSourceToIntersect * (Length * 0.975f);// Bod ve 195% vzdálenosti od světla ve směru průsečíku
pt += m_LightSourcePos;
RenderGlow(0.4f, 0.1f, 0.9f, 0.5f, pt, 2.0f);// Vykreslení záře
}
// Obnovení nastavení OpenGL
glDisable(GL_BLEND);
glEnable(GL_DEPTH_TEST);
glDisable(GL_TEXTURE_2D);
}
}
Následuje výpis kódu pro rendering čočkové záře. Máme celkem čtyři různé funkce, které se ale liší pouze texturou objektu, jinak jsou identické.
void glCamera::RenderHalo(GLfloat r, GLfloat g, GLfloat b, GLfloat a, glPoint p, GLfloat scale)// Vykreslení záře
{
glPoint q[4];// Pomocný bod
q[0].x = (p.x - scale);// Výpočet pozice
q[0].y = (p.y - scale);
q[1].x = (p.x - scale);
q[1].y = (p.y + scale);
q[2].x = (p.x + scale);
q[2].y = (p.y - scale);
q[3].x = (p.x + scale);
q[3].y = (p.y + scale);
glPushMatrix();// Uložení matice
glTranslatef(p.x, p.y, p.z);// Přesun na pozici
glRotatef(-m_HeadingDegrees, 0.0f, 1.0f, 0.0f);// Odstranění rotací
glRotatef(-m_PitchDegrees, 1.0f, 0.0f, 0.0f);
glBindTexture(GL_TEXTURE_2D, m_HaloTexture);// Textura
glColor4f(r, g, b, a);// Nastavení barvy
glBegin(GL_TRIANGLE_STRIP);
glTexCoord2f(0.0f, 0.0f); glVertex2f(q[0].x, q[0].y);
glTexCoord2f(0.0f, 1.0f); glVertex2f(q[1].x, q[1].y);
glTexCoord2f(1.0f, 0.0f); glVertex2f(q[2].x, q[2].y);
glTexCoord2f(1.0f, 1.0f); glVertex2f(q[3].x, q[3].y);
glEnd();
glPopMatrix();// Obnovení matice
}
Tak to by z kódu bylo všechno. Pomocí kláves W, S, A, D můžete v programu měnit směr kamery. Klávesy 1 a 2 zapínají/vypínají výpisy informací. Z a C nastavují kameře konstantní rychlost a X ji zastavuje.
Samozřejmě nejsem první člověk, který vytvářel čočkové efekty, a proto můžete dole najít pár odkazů, které mi při psaní pomohly. Chtěl bych také poděkovat Davu Steerovi, Cameron Tidwell, Bertu Sammonsovi a Brannon Martidale za zpětnou vazbu a testování kódu na rozličném hardware.
- http://www.gamedev.net/reference/articles/article874.asp
- http://www.gamedev.net/reference/articles/article813.asp
- http://www.opengl.org/developers/code/mjktips/lensflare/
- http://www.markmorley.com/opengl/frustumculling.html
- http://oss.sgi.com/projects/ogl-sample/registry/HP/occlusion_test.txt
- http://oss.sgi.com/projects/ogl-sample/registry/NV/occlusion_query.txt
napsal: Vic Hollis <vichollis (zavináč) comcast.netVic>
přeložil: Michal Turek - Woq <WOQ (zavináč) seznam.cz>
Poznámky Daria Corna - rIO ze Spinning Kids
Přidal jsem několik testů pro zjištění objektů ve scéně před čočkovým efektem (na pozici zdroje světla). V takovém případě se záře vypíná. Nový kód by měl být dobře okomentován a je označen řetězcem # New Stuff #. Jeho případné odstranění by nemělo činit problémy. Modifikace jsou následující:
- Nová metoda třídy glCamera nazvaná IsOccluded(), která vrací true v případě, že se před světlem nachází nějaký objekt
- Několik proměnných pro gluCylinder (použit jako objekt stínící světlu)
- Změny v glDraw() pro vykreslení stínícího objektu
- Deinicializační kód pro quadratic
Doufám, že se vám modifikovaná verze bude líbit více. Jako domácí úkol si můžete zkusil testovat více než jeden bod na souřadnicích světla, aby se záře skokově nevypínala, ale postupně mizela.
Zdrojové kódy
- Visual C++ kód této lekce.
- Borland C++ Builder 6 kód této lekce. ( Le Thanh Cong )
- Dev C++ kód této lekce. ( Michael Small )
- Code Warrior 5.3 kód této lekce. ( Scott Lupton )
- Visual Studio .NET kód této lekce. ( Joachim Rohde )
- Lesson 44 - With Extension Support (VC++).