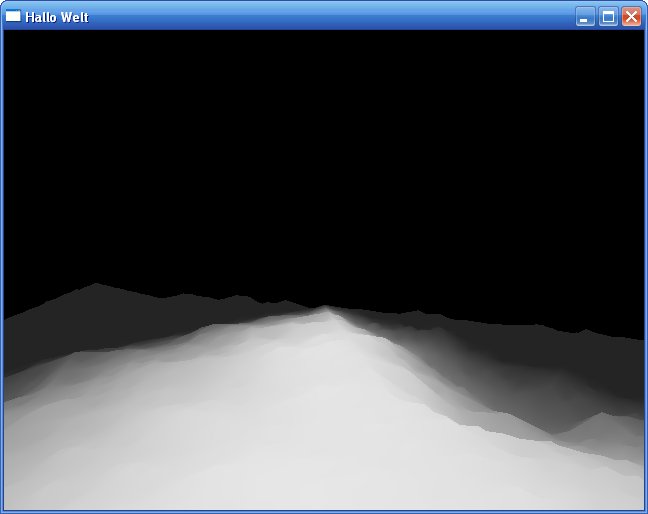
Procedurálne generovanie terénu

Možno ste už počuli o výškových mapách. Sú to také čiernobiele obrázky, pomocou ktorých sa vytvára 3D terén (výška terénu na určitej pozícii je určená farbou zodpovedajúceho bodu na výškovej mape). Najjednoduchšie je výškovú mapu načítať zo súboru a je pokoj. Sú však situácie, ako napr. keď robíte grafické demo, ktoré má byť čo najmenšie, keď príde vhod výškovú mapu vygenerovať procedurálne. Takže si ukážeme ako na to. Ešte snáď spomeniem že čítať ďalej môžu aj tí, ktorí chcú vedieť ako vygenerovať takzvané "oblaky" (niekedy sa tomu hovorí aj plazma), nakoľko tento tutoriál bude z veľkej časti práve o tom.

Naša výšková mapa bude vyzerať približne takto:

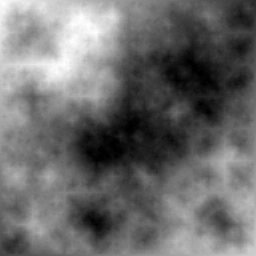
Takže ako to teda funguje? Prvú vec, ktorú by ste mali poznať, je rekurzia. Pre tých, ktorí nevedia čo to je, skúsim v krátkosti vysvetliť. Rekurzia je, keď nejaká procedúra alebo funkcia zavolá sama seba. Príklad:

procedure davaj(x: integer);
begin
	writeln(x);
	if x < 10 then davaj(x+1);
end;

Tato procedúra spravi to, že vypíšu všetky čísla od X do 10 (takža davaj(3); vypíše čísla od 3 do 10). To if x < 10 zabezpečí, že keď bude procedúra zavolaná s parametrom väčším alebo rovným 10, procedúra nebude ďalej volať sama seba. Niesom si istý, tuším sa tomu hovorí návrat z rekurzie alebo tak nejako, podstatné je to, že bez toho by rekurzívna procedúra volala sama seba donekonečna, čo by viedlo k pádu programu (pre nedostatok pamäte). Na túto vec treba vždy pri písaní rekurzívnych procedúr myslieť, aby vám niekedy skončili.

Takže toľko vsuvka o rekurzii, teraz spať k vytváraniu výškovej mapy. Algorytmus je taký, že procedúra dostane ako parametre súradnice obdĺžnika, ktorý chceme vyplniť oblakmi, rozdelí ho na 4 menšie obdĺžniky a zavolá sama seba na každý z nich. Situácia vyzerá takto:

[X1,Y1]       [X2,Y1]
Cl1-------1-------Cl2
  |       |       |
  |       |       |
  3-------5-------4
  |       |       |
  |       |       |
Cl3-------2-------Cl4
[X1,Y2]       [X2,Y2]

Funkcia dostane ako parametre X1,Y1,X2,Y2, čo sú súradnice obdĺžnika, ktorý chceme vyplniť. Najskôr skontroluje, či náhodou jeho rozmer nieje menší ako 2x2, ak áno, ukončí sa (to bude návrat z rekurzie). Potom stredu každej strany (1,2,3,4) nastaví farbu, ktorá je rovná priemeru farieb koncových bodov tejto strany (takže farba bodu 1 bude (cl1+cl2)/2..atď) a stredu obdĺžnika nastaví farbu rovnú priemeru farieb jeho rohov, teda (cl1+cl2+cl3+cl4)/4. K tejto farbe potom pripočíta/odpočíta náhodné číslo, ktorého veľkosť bude závisieť od veľkosti obdĺžnika. No a nakoniec zavolá 4 krát sama seba na všetky štyri obdĺžniky ktoré vynikli "rozdelením" pôvodného obdĺžnika (cl1,1,5,3; 1,cl2,4,5; 3,5,2,cl3; 5,4,cl4,2). To je celé.

Teraz si ukážeme ako to bude vyzerať prakticky (prakticky = ako to zapísať v Delphi; týmto sa zároveň ospravedlňujem všetkým céčkarom, ale keď niekto používa tak hackerský jazyk ako C alebo nebodaj C++, určite pochopí aj ten pascalovský kód ;)). Najskôr treba poriešiť, kam budeme našu výškovú mapu generovať. Ja som použil globálne jednorozmerné dynamické pole, (aby som mohol jednoducho meniť veľkosť mapy, ale ak chcete, kľudne môžete použiť aj statické pole, alebo si alokovať pamäť tými vašimi malloc-mi a getmem-ami), ktoré pomenujeme poeticky _.

var	_: array of byte;
	width: integer;//premenná width bude obsahovať šírku aj výšku štvorcovej mapy

Pred samotným aktom tvorenia procedúry, ktorá sa bude starať o vygenerovanie oblakov do nášho poľa, napíšeme si zopár pomocných procedúr:

Function Interval(Value,Min,Max: Integer): Integer;
//oseka value tak aby bola v intervale <min,max>
Begin
	Interval:=Value;
	If Value < Min then Interval:=Min;
	If Value > Max then Interval:=Max;
End;

Function Md(Cl1,Cl2: Byte): Byte;
//vrati priemer cl1 a cl2
var T: Integer;
Begin
	T:=(Cl1 + Cl2) div 2;
	Md:=T;
End;

Function FF(X1,Y1,X2,Y2: Integer): Integer;
//parametre tejto funkcie su suradnice obdlznika
//funkcia vrati nahodne cislo; cim je obdlznik
//s lavym hornym rohom [X1,Y1] a pravym dolnym
//rohom [X2,Y2] mensi, tym bude nahodne cislo mensie
Var M: Byte;
Begin
	M:=Random(2);
	if M=0 then FF:=Round(Random((ABS(X2-X1)+ABS(Y2-Y1)))*0.5)
	else FF:=-Round(Random((ABS(X2-X1)+ABS(Y2-Y1)))*0.5);
End;

Skôr ako začneme, musíme si ešte ujasniť jednu vec. Zjavne ideme generovať dvojrozmerný (2D) obrázok, a chceme ho mať uložený v 1 rozmernom poli. Takže otázka znie, aký je index poľa pre bod so súradnicami [X,Y]? Nebudem vás napínať, je to takto:

Pole[Y * sirka + X]

Tudíž keď chceme bodu na súradniciach [X,Y] nastaviť farbu F, napíšeme

_[Y * Width + X]:=F;

Teraz máme všetko čo potrebujeme na to, aby sme mohli napísať našu rekurzívnu funkciu, ktorá nám vygeneruje oblaky. Nazveme si ju Divide. Tu je okomentovaný zdroják:

Procedure Divide(X1,Y1,X2,Y2: Integer);
// procedura vlozi do vyskovej mapy 5 bodov:
//
// 1 - stred strany [X1,Y1][X2,Y1], bude mat farbu (Cl1+Cl2) div 2
// 2 - stred strany [X1,Y2][X2,Y2], bude mat farbu (Cl3+Cl4) div 2
// 3 - stred strany [X1,Y1][X1,Y2], bude mat farbu (Cl1+Cl3) div 2
// 4 - stred strany [X2,Y1][X2,Y2], bude mat farbu (Cl2+Cl4) div 2
// 5 - stred obdlznika, bude mat farbu (1+2+3+4) div 4 + FF
//
// [X1,Y1]       [X2,Y1]
// Cl1-------1-------Cl2
//   |       |       |
//   |       |       |
//   3-------5-------4
//   |       |       |
//   |       |       |
// Cl3-------2-------Cl4
// [X1,Y2]       [X2,Y2]
//
// potom rekurzivne zavola sama seba na vsetky 4 obdlzniky
// (cl1,1,5,3; 1,cl2,4,5; 3,5,2,cl3; 5,4,cl4,2)
//
// tym vyplni oblakmi cely obdlznik, na ktory bola povodne zavolana

Var	Cl1,Cl2,Cl3,Cl4,	//farby v rohoch obdlznika
	C1,C2,C3,C4: Byte;	//farby s stredoch stran
	NX,NY: Integer;		//suradnice stredu obdlznika
Begin
	//nacitanie farieb v rohoch obdlznika
	Cl1:=_[Y1*Width+X1];
	Cl2:=_[Y1*Width+X2];
	Cl3:=_[Y2*Width+X1];
	Cl4:=_[Y2*Width+X2];

	//ak je obdlznik mensi ako 2x2, nieje co vykreslovat
	//a procedura moze skoncit, keby tu tento riadok nebol,
	//rekurzia by nikdy neskoncila
	if (ABS(X2-X1)<2) and (Y2-Y1<2) then Exit;

	//stred obdlznika
	NX:=Round((X1+X2)/2);
	NY:=Round((Y1+Y2)/2);

	//stredy stran
	C1:=Md(Cl1,Cl2);_[Y1*Width+NX]:=C1;
	C2:=Md(Cl3,Cl4);_[Y2*Width+NX]:=C2;
	C3:=Md(Cl1,Cl3);_[NY*Width+X1]:=C3;
	C4:=Md(Cl2,Cl4);_[NY*Width+X2]:=C4;

	//stred obdlznika (ff je nahodne cislo,
	// tym mensie cim mensi je obdlznik)
	_[NY*Width+NX]:=Interval(Md(Md(Cl1,Cl2),
		Md(Cl3,Cl4))+FF(X1,Y1,X2,Y2),0,255 );

	//rekurzia (zabezpeci aby sa vyplnik cely obdlznik)
	Divide(X1,Y1,NX,NY);
	Divide(NX,Y1,X2,NY);
	Divide(X1,NY,NX,Y2);
	Divide(NX,NY,X2,Y2);
End;

Možno ste si všimli, že celé oblaky závisia od toho, akej farby sú v rohoch výškovej mapy. Takže pred samotným zavolaním procedúry Divide im nastavíme náhodné hodnoty:

Procedure GenClouds;
//procedura do pola _ vygeneruje oblaky - vyskovu mapu
Begin
	Randomize;

	//rohom nastavime nahodne hodnoty
	//budu mat vplyv na tvar celeho terenu
	_[0*Width+0]:=Random(64);
	_[0*Width+Width-1]:=Random(64);
	_[(Width-1)*Width+0]:=Random(64);
	_[(Width-1)*Width+Width-1]:=Random(64);

	//vykreslenie oblakov
	Divide(0,0,Width-1,Width-1);
End;

Ak sa čudujete prečo tam je random(64) a nie random(256), tak vedzte, že je to tak kôli tomu, aby bol terén na okrajoch nižší (to kôli kamere, ktorá bude lietať okolo terénu). Preto sa prosím nesnažte v tom hľadať nejaký hlbší význam.

Pre istotu si ešte ukážeme, ako náš vysnený terén vyrenderovať pomocou OpenGL. Konkrétne si ukážeme hneď dva spôsoby. Na prvý budeme potrebovať ďalšie dve procedúry. Tieto procedúry použijeme, keď budeme chcieť vyrátať normálový vektor ľubovolného trojuholníka - to sa hodí, keď chceme scénu osvetliť:

Definujeme si aj štruktúru TCoord3D, do ktorej si môžeme uložiť súradnice bodu alebo vektora:

TYPE TCoord3D = RECORD
	X,Y,Z: GLfloat;
END;

procedure Normalize(var Vector: TCoord3D);
//procedura normalizuje vektor
var Len: GLfloat;
begin
	//dlzka vektora
	Len:=SQRT(SQR(Vector.X)+SQR(Vector.Y)+SQR(Vector.Z));

	if Len=0 then Exit;

	//vypocet normalizovaneho <0,1> vektora
	Vector.X:=Vector.X/Len;
	Vector.Y:=Vector.Y/Len;
	Vector.Z:=Vector.Z/Len;
end;

procedure CalcNormal(P1,P2,P3: TCoord3D; var Res: TCoord3D);
//procedura vypocita normalovy vektor
//trojuholnika a ulozi ho do premennej Res
var V1,V2: TCoord3D;
begin
	//vypocitanie dvoch vektorov trojuholnika
	V1.X:=P1.X - P2.X;
	V1.Y:=P1.Y - P2.Y;
	V1.Z:=P1.Z - P2.Z;

	V2.X:=P2.X - P3.X;
	V2.Y:=P2.Y - P3.Y;
	V2.Z:=P2.Z - P3.Z;

	//vektorovy sucin
	Res.X:=V1.Y*V2.Z - V1.Z*V2.Y;
	Res.Y:=V1.Z*V2.X - V1.X*V2.Z;
	Res.Z:=V1.X*V2.Y - V1.Y*V2.X;

	Normalize(Res);
end;

Terén budeme vykresľovať po trojuholníkoch - každej štvorici bodov ([X,Y], [X+1,Y], [X+1,Y] a [X+1,Y+1]) na výškovej mape budú zodpovedať dva trojuholníky. Takže nám stačí prebehnúť pole dvoma vnorenými cyklami. No a takto to bude vyzerať:

function DrawGLScene(): BOOL; {vykreslenie 3D sceny}
var C,E: Integer;
    Norm: TCoord3D; // normalovy vektor
    P: Array[0..2] of TCoord3D; //suradnice vrcholov vykreslovaneho trojuholnika
begin

	glClear(GL_COLOR_BUFFER_BIT or GL_DEPTH_BUFFER_BIT);

	glLoadIdentity();
	glTranslatef(0.0,0.0,-2);
	glRotatef(--Angle,0.0,1.0,0.0);

	glBegin(GL_TRIANGLES);

	for E:=0 to Width-2 do
		for C:=0 to Width-2 do begin
			//prvy trojuholnik

			//vyratame si suradnice trojuholnika, ktory chceme vykreslit
			//suradnice Y (vysky) zavysia od hodnot vo vyskovej mape (logicky)
			//celkova vyska terenu je este zredukovana pomocou toho /Width/1.5

			//pri vypocte suradnic X a Z si vsimnite to /Width*4
			//to nam zabezpeci, ze bez ohladu na velkost vyskovej mapy
			//bude mat vyrenderovany teren sirku aj dlzku 4
			//v opengl jednotkach)

			//mimochodom shr 1 (shift right) robi bitovy posun doprava,
			//v tomto pripade o 1 bit; takze shr 1 je to iste ako div 2, ale
			//o nieco rychlejsie (procak tusim tuto operaciu priamo podporuje)

			P[0].X:=(C-(Width shr 1))/Width*4;
			P[0].Y:=-0.5+(_[(E)*Width+C]/Width/1.5);
			P[0].Z:=(E-(Width shr 1))/Width*4;

			P[1].X:=(C-(Width shr 1)+1)/Width*4;
			P[1].Y:=-0.5+(_[(E)*Width+C+1]/Width/1.5);
			P[1].Z:=(E-(Width shr 1))/Width*4;

			P[2].X:=(C-(Width shr 1)+1)/Width*4;
			P[2].Y:=-0.5+(_[(E+1)*Width+C+1]/Width/1.5);
			P[2].Z:=(E-(Width shr 1)+1)/Width*4;

			//ak nechceme mat teren vyhladeny, vyrateme si normalu trojuholnika
			//a nastavime ju

			if Not Smooth then begin
				CalcNormal(P[2],P[1],P[0], Norm);
				glNormal3f(Norm.X,Norm.Y,Norm.Z);
			end;

			//ak chceme teren vyhladeny, pre kazdy vertex nastavime normalu, ktora
			//bude vlastne normalizovany ekvivalent vektora s rovnakymi suradnicami
			//ako samotny vertex (mimochodom ked si takymto sposobom onormalujete
			//kocku a nechate ju rotovat, dostanete celkom posobivy vysledok)

			//ako bonus nastavime vertext farbu podla jeho vysky, aby sme teren
			//videli aj s vypnutym svetlom

			if Smooth then begin
				Norm:=P[0];
				Normalize(Norm);
				glNormal3f(Norm.X,Norm.Y,Norm.Z);
			end;
			glColor3f(0.3,0.5+P[0].Y,0.0);
			glVertex3f(P[0].X,P[0].Y,P[0].Z);

			if Smooth then begin
				Norm:=P[1];
				Normalize(Norm);
				glNormal3f(Norm.X,Norm.Y,Norm.Z);
			end;
			glColor3f(0.3,0.5+P[1].Y,0.0);
			glVertex3f(P[1].X,P[1].Y,P[1].Z);

			if Smooth then begin
				Norm:=P[2];
				Normalize(Norm);
				glNormal3f(Norm.X,Norm.Y,Norm.Z);
			end;
			glColor3f(0.3,0.5+P[2].Y,0.0);
			glVertex3f(P[2].X,P[2].Y,P[2].Z);

			//druhy trojuholnik
			P[0].X:=(C-(Width shr 1))/Width*4;
			P[0].Y:=-0.5+(_[(E)*Width+C]/Width/1.5);
			P[0].Z:=(E-(Width shr 1))/Width*4;

			P[1].X:=(C-(Width shr 1)+1)/Width*4;
			P[1].Y:=-0.5+(_[(E+1)*Width+C+1]/Width/1.5);
			P[1].Z:=(E-(Width shr 1)+1)/Width*4;

			P[2].X:=(C-(Width shr 1))/Width*4;
			P[2].Y:=-0.5+(_[(E+1)*Width+C]/Width/1.5);
			P[2].Z:=(E-(Width shr 1)+1)/Width*4;

			if Not Smooth then begin
				CalcNormal(P[2],P[1],P[0], Norm);
				glNormal3f(Norm.X,Norm.Y,Norm.Z);
			end;

			if Smooth then begin
				Norm:=P[0];
				Normalize(Norm);
				glNormal3f(Norm.X,Norm.Y,Norm.Z);
			end;
			glColor3f(0.3,0.5+P[0].Y,0.0);
			glVertex3f(P[0].X,P[0].Y,P[0].Z);

			if Smooth then begin
				Norm:=P[1];
				Normalize(Norm);
				glNormal3f(Norm.X,Norm.Y,Norm.Z);
			end;
			glColor3f(0.3,0.5+P[1].Y,0.0);
			glVertex3f(P[1].X,P[1].Y,P[1].Z);

			if Smooth then begin
				Norm:=P[2];
				Normalize(Norm);
				glNormal3f(Norm.X,Norm.Y,Norm.Z);
			end;
			glColor3f(0.3,0.5+P[2].Y,0.0);
			glVertex3f(P[2].X,P[2].Y,P[2].Z);
		end;

	glEnd();

	Angle:=Angle+(0.5/FPS);

	Result:=TRUE;// OK
end;

Z komentárov by malo byť všetko jasné. Snáď len toľko, že treba niekde zadefinovať premennú Smooth typu boolean, ktorá určuje, či sa má terén vykresľovať vyhľadený alebo nie.

napsal: Peter Mindek <2mindo (zavináč) gmail.com>

Zdrojové kódy

• 21.7 kB - Delphi

Komerční publikování v tištěné, elektronické nebo jiné podobě je bez výslovného souhlasu zakázáno. Redistribuce pro výukové účely nebo osobní použití je však povolena.