Octree
Octree (octal tree, oktalový strom) je způsob rozdělování 3D prostoru na oblasti, který umožňuje vykreslit pouze tu část světa/levelu/scény, která se nachází ve výhledu kamery, a tím značně urychlit rendering. Může se také použít k detekcím kolizí.
Popis octree
Příklad, proč je rozdělování prostoru tak nezbytné... Předpokládejme, že pro hru vytváříme kompletní 3D svět, který se skládá z více jak 100 000 polygonů. Kdybychom je při každém překreslení scény v cyklu posílali na grafickou kartu úplně všechny, FPS by zcela určitě kleslo na absolutní minimum a aplikace byla extrémně trhaná. Na absolutně nejnovějších kartách by to nemuselo být zase tak strašné, ale proč se omezovat jen na uživatele, kteří si mohou dovolit grafickou kartu za deset tisíc a více? Někdy, dokonce i když máte opravdu rychlou grafickou kartu, může hodně zpomalovat samotný cyklus posílající data. Nenašla by se nějaká cesta, jak renderovat pouze polygony ve výhledu kamery? To je právě největší výhodou octree - umožňuje RYCHLE najít viditelné polygony a vykreslit je.
Jak octree pracuje
Octree pracuje pomocí krychlí. Začínáme kořenovým uzlem (root node), což je krychle, jejíž stěny jsou rovnoběžné se souřadnicovými osami a která v sobě zahrnuje kompletně celý svět, level nebo scénu. Když si okolo celého herního světa představíte velkou neviditelnou krychli, určitě se nezmýlíte.
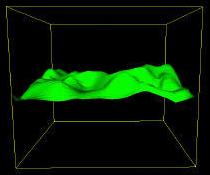
Kořenový uzel ukládá všechny vertexy celého světa. Vzato kolem a kolem, toto je nám zatím naprosto k ničemu, takže ho zkusíme rozdělit na osm menších (odsud slovo octree - octal tree), které ji budou kompletně vyplňovat.
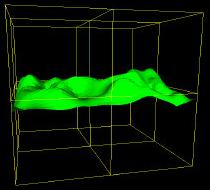
Prvním dělením jsme rozdělili svět na osm menších částí. Umíte si představit, kolik jich bude po dvou, třech nebo čtyřech děleních? Ze světa se stane spousta malých krychliček. Ale k čemu to vlastně je, kam zmizel ten nárůst rychlosti u vykreslování? Představte si, že se kamera nachází přesně ve středu světa a v záběru má pravý dolní roh. z linek je jasně patrně, že jsou vidět pouze čtyři z osmi uzlů v octree. Jedná se o dvě horní a dvě spodní zadní krychle. Z toho všeho vyplývá, že stačí vykreslit pouze vertexy uložené v těchto čtyřech uzlech.

Ale jak zjistit, které uzly půjdou vidět a které ne? Budete se divit, ale odpověď je velice snadná - frustum culling. Stačí získat rozměry výhledu kamery a potom otestovat každou krychli, jestli ho protíná popř. leží celá uvnitř. Pokud ano, vykreslíme všechny vertexy, které jsou přiřazeny tomuto uzlu. V příkladu výše jsme získali nárůst výkonu o 50% a to jsme dělili pouze jednou. Čím více dělení bude, tím dosáhneme větší přesnosti (na bod). Samozřejmě musíme vytvořit optimální počet uzlů, protože přespříliš rekurzivních testů by zpomalovalo možná více, než kdyby nebyly žádné. Zkusme rozdělit každou z dosavadních osmi krychlí na dalších "osm".
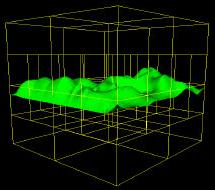
Určitě jste si všimli změny oproti minulému dělení. V této úrovni už je zbytečná VYTVÁŘET v každé z osmi původních krychlí dalších OSM, horní a spodní část může zůstat nerozdělena. Vždy zkoušíme rozdělit uzel na osm další, ale pokud se už v této oblasti nevyskytují žádné trojúhelníky, ignorujeme ji a ani už pro ni nealokujeme žádnou další paměť. Čím více prostor rozdělujeme, tím více uzly kopírují originální svět. Na následujících obrázcích jsou vyobrazeny dvě koule, každá na opačné straně. Po prvním dělení se kořenový uzel rozdělí pouze na dva poduzly, ne na osm. Po dalších děleních krychle kopírují objekty mnohem více. Nové uzly se vytvářejí pouze tehdy, jsou-li potřeba, v daném prostoru se musí nacházet objekty.
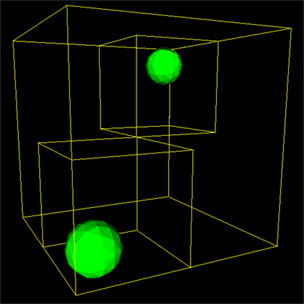

Kdy ukončit dělení
Nyní už byste měli chápat, jak dělení pracuje, ale ještě nevíte, kdy ho zastavit, aby rekurze neprobíhala do nekonečna. Existují tři základní způsoby.
První spočívá v ukončení rozdělování uzlu, pokud je počet jeho trojúhelníků menší než maximální počet (například sto). Pokud jich bude méně, ukončíme dělení a všechny zbývající trojúhelníky přiřadíme tomuto uzlu. Z toho plyne, že trojúhelníky obsahují VÝHRADNĚ koncové uzly. Po rozdělení na další úroveň nepřiřadíme trojúhelníky rodičovskému uzlu, ale jeho potomkům případně až potomkům jeho potomků atd.
Další možností, jak ukončit rekurzi, je definovat určitou maximální úroveň dělení. Můžeme si například zvolit maximální hloubku rekurze deset a po jejím přesažení přiřadíme zbývající trojúhelníky koncovým uzlům.
Třetím způsobem je test maximálního počtu uzlů, může jich být např. 500. Před každým vytvořením nového uzlu, inkrementujeme čítač jejich počtu a otestujeme, jestli je jejich celkový počet větší než 500. Pokud ano, dělit dále nebudeme a přiřadíme koncovým uzlům všechny zbývající trojúhelníky.
Osobně používám kombinaci první a třetí metody, ale pro začátek může být dobrým nápadem zkusit první a druhou, takže budete moci testovat různé úrovně dělení vizuálně i manuálně.
Jak vykreslit octree
Jakmile octree jednou vytvoříme, máme možnost vykreslovat pouze uzly, které se nacházejí ve výhledu kamery. Počet trojúhelníků v uzlu jsme se snažili co nejvíce minimalizovat, protože musíme vykreslit i částečně viditelné krychle - kvůli přesahujícímu rožku renderovat tisíce trojúhelníků. Vždy začínáme od kořenového uzlu, pro každý, na nižší úrovni, máme uloženy souřadnice jeho středu a šířku. Tato organizace dat se skvěle hodí pro předání do funkce jako
bool CubeInFrustum(float x, float y, float z, float size);// Je krychle viditelná?
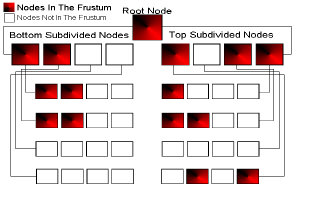
..., která vrátí true nebo false podle toho, jestli by krychle po vykreslení byla vidět nebo ne. Pokud ano, stejným způsobem otestujeme všechny její poduzly, v opačném případě ignorujeme celou větev stromu. Testy provádíme rekurzivně až po koncové uzly, u nichž v případě viditelnosti vykreslíme všechny vertexy, které obsahují. Opět opakuji, že vertexy jsou uloženy pouze v koncových uzlech. Obrázek dole ukazuje průchod skrz dvouúrovňový octree. Červené obdélníky představují viditelné uzly, bílé nejsou vidět.
Na první pohled dojdeme k závěru, že čím více úrovní vytvoříme, tím méně trojúhelníků budeme muset renderovat. Pokud by trojúhelníky byly rovnoměrně rozložené, při aktuálním pohledu kamery by se jich u kořenového uzlu vykreslovalo 100 procent (jeden z jednoho uzlu), v první úrovni 62 procent (pět z osmi uzlů) a v poslední úrovni 28 procent (devět z 32 uzlů; respektive z 64, ale polovina neobsahovala trojúhelníky, takže nebyly vytvořeny).
Tato čísla ale berte s velkou rezervou, protože záleží na pozici a natočení kamery. Pokud by byl v záběru kompletně celý svět (pohled z dostatečně vzdáleného externího bodu), nejen, že by nedocházelo k žádné rychlostní optimalizaci, ale kvůli spoustě dodatečných výpočtů by se celý rendering výrazně zpomalil - čím více uzlů, tím více "zbytečných" testů, které neodstraní žádné trojúhelníky. Nicméně, abych vás nestrašil, neznám hru, která by umožňovala opustit herní svět a dívat se z venku, takže se s největší pravděpodobností vždy nějaké uzly ořežou. Někdy jich bude více jindy méně.
Kolize s octree
Octree sice primárně slouží pro rendering, ale stejně tak dobře se může použít i pro detekci kolizí. Programové techniky kolizí se liší od hry ke hře, takže asi budete chtít naprogramovat vlastní algoritmus, který bude vašemu enginu plně vyhovovat. Základem je funkce, která z octree vrátí všechny vertexy nacházející se v blízkosti předaného bodu. Měl by jím být střed postavy nebo objektu. Potíže nastanou v blízkosti okraje uzlu, kde objekt bez problémů prochází skrz netestované vertexy ze sousedního. Řešení je opět hned několik. Spolu s bodem můžeme předat buď poloměr nebo bounding box a potom zjistit kolize s uzly v octree. Vše závisí na tvaru testovaného objektu. Příklad několika funkčních prototypů:
CVector3* GetVerticesFromPoint(float x, float y, float z);// Vertexy z uzlu octree
CVector3* GetVerticesFromPointAndRadius(float x, float y, float z, float radius);// Vertexy z kulové oblasti
CVector3* GetVerticesFromPointAndCube(float x, float y, float z, float size);// Vertexy k krychlové oblasti
Jsem si jistý, že vás právě napadly i mnohem lepší způsoby kolizí, ale na začátku se snadněji implementují jednoduché techniky. Jakmile jednou máte k dispozici vertexy v dané oblasti, můžete provést mnohem přesnější výpočty. Ještě jednou... když přijde na různé typy kolizí, vždy nejvíce záleží na tom, jak aplikace pracuje.
napsal: Ben Humphrey - DigiBen <digiben (zavináč) gametutorials.com>
přeložil: Michal Turek - Woq <WOQ (zavináč) seznam.cz>, 12.07.2004
Anglický originál článku: http://www.gametutorials.com/Tutorials/OpenGL/Octree.htm
Zdrojové kódy
- Najdete na http://www.gametutorials.com/ v sekci Tutorials -> OpenGL
- Frustum culling je dostupný na stejné adrese, byl popsán také v NeHe Tutoriálu 44