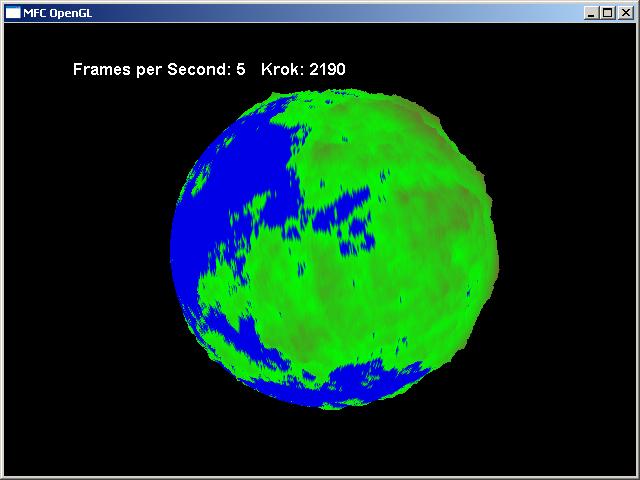
Generování planet
Pokud budete někdy potřebovat pro svou aplikaci vygenerovat realisticky vypadající planetu, tento článek se vám bude určitě hodit - popisuje jeden ze způsobů vytváření nedeformovaných kontinentů. Obvyklé způsoby pokrývání koule rovinnou texturou končí obrovskými deformacemi na pólech. Další nevýhodou některých způsobů je, že výsledek je orientován v nějakém směru. To u této metody nehrozí.
Postup
Princip je jednoduchý, horší ale bude implementace. Jak tedy postupovat?
- Vezmeme kouli
- Náhodně zvolenou rovinou procházející přes její střed, ji rozdělíme na dvě poloviny
- Jednu polovinu o trochu zvětšíme a druhou zmenšíme
- Opakujeme kroky 2 a 3





Po velkém počtu dělení se začnou malé hřebeny formovat do tvaru kontinentů, takže nechte algoritmus probíhat tak dlouho, dokud nemají požadovaný tvar.






Nedostatky
Jistě jste si všimli něčeho podivného. Pohled zezadu vypadá skoro stejně jako čelní strana vzhůru nohama a s prohozenými kontinenty za oceány. To je asi největší nevýhoda této metody. Na místě, kde se na jedné straně planety nacházejí moře, je na druhé straně kontinent, nicméně si toho často ani nevšimnete.
Implementace
Nejdříve si musíme nadefinovat "kouli" s možností proměnného poloměru. Uděláme to pomocí dvourozměrného pole m_r - viz následující výpis hlavičkového souboru. Můžeme si to dovolit, protože každý bod v prostoru je dán dvěma úhly a vzdáleností od středu. První index pole udává úhel alfa, druhý index představuje úhel beta a hodnota uložená v poli vyjadřuje vzdálenost od středu. Úhel alfa udává odklon spojnice bodu a počátkem s osou x v rovině x, z. Úhel beta udává úhel mezi spojnicí bodu a počátkem s osou y. Předpokládáme klasickou orientaci souřadnic v OpenGL, tj. x doprava, y nahoru a z ven z obrazovky (k uživateli). Pro přepočet indexů pole na úhel používáme následující makro:
#define UHEL(x) (2 * PI * (double(x) / double(SLICES)))
...kde x je index pole, PI je hodnota 3.14159... a SLICES udává v kolika bodech na obvodu je koule definovaná, tj. počet poledníků. Počet rovnoběžek je poloviční, aby byl zjednodušený kód pro vykreslování a výpočet úhlu z indexu. Pro výpočet souřadnic z úhlů a poloměru se používají následující vzorce:
x = r * cos(alfa) * sin(beta)
y = r * cos(beta)
z = r * sin(alfa) * sin(beta)
A zde je slibovaný výpis hlavičkového souboru.
// na kolik částí je planeta rozdělena
// počet poledníků je roven SLICES
// počet rovnoběžek je roven SLICES / 2
// čím je hodnota větší, tím déle trvá výpočet a vykreslování, ale zároveň se zlepšuje vzhled
#define SLICES 500
// poloměr hladiny oceánů - nastavuje se pomocí funkce Reset
// (je volána automaticky v konstruktoru, ale můžete ji volat i sami)
#define R m_default_r
#define PI 3.1415926535897932384626433832795
// přepočet indexu pole na úhel
#define UHEL(x) (2 * PI * (double(x) / double(SLICES)))
class CPlanet
{
public:
// funkce pro generování kontinentů
// nsteps udává kolik kroků algoritmu pro generování provést
// pěkné výsledky lze dostat asi od 250 kroků
void GenerujKontinenty(const int nsteps);
// resetuje do výchozího stavu a nastaví poloměr planety
void Reset(const double r);
// vykreslí planetu (pomocí OpenGL)
void Draw();
CPlanet();
virtual ~CPlanet();
protected:
// pomocná proměnná do které se ukládá výška nejvyššího vrcholu kvůli volbě barvy při vykreslování
double m_max_r;
// pole pro uložení výšky povrchu
double m_r[SLICES][SLICES/2];
// výchozí poloměr planety a zároveň výška hladiny moří
double m_default_r;
};
Funkce která implementuje generování kontinentů vypadá takto:
void CPlanet::GenerujKontinenty(const int nsteps)
{
m_max_r = R;
int i,j,k;
double nx,ny,nz,x,y,z,ns;
for (k=0; k<nsteps; k++)// opakovat po zadaný počet kroků
{
// náhodně vygenerovat normálový vektor plochy
nx = (double(rand())/double(RAND_MAX))-0.5;
ny = (double(rand())/double(RAND_MAX))-0.5;
nz = (double(rand())/double(RAND_MAX))-0.5;
// pro všechny vrcholy
for(i=0; i<SLICES; i++)
for(j=0; j<SLICES/2; j++)
{
// vektor (jednotkový) ze středu koule k vrcholu
x = cos(UHEL(i))*sin(UHEL(j));
y = cos(UHEL(j));
z = sin(UHEL(i))*sin(UHEL(j));
// skalární součin normálového vektoru a vektoru ze středu koule k vrcholu
// pokud je úhel mezi vektory menší nebo roven 90 stupňů je kladný, jinak záporný
ns = nx*x + ny*y + nz*z;
if (ns>=0)// úhel mezi vektory menší nebo roven 90 stupňů
{
// zvýšit vrchol
m_r[i][j] += 1e-3*R;
}
else// úhel mezi vektory větší než 90 stupňů
{
// snížit vrchol
m_r[i][j] -= 1e-3*R;
}
// pomocný krok kvůli volbě barvy vrcholu
// pokud je výška vrcholu větší než maximální potom maximální nastavit na výšku vrcholu
if (m_max_r<m_r[i][j]) m_max_r=m_r[i][j];
}
}
}
Teď je ještě třeba na základě takto spočítaných hodnot planetu vykreslit.
void CPlanet::Draw()
{
register int i,j;
// vykreslení koule s různými poloměry jednotlivých bodů
glBegin(GL_TRIANGLE_STRIP);
if (m_r[0][0] <= R)// pod hladinou moře
{
glColor3d(0, 0, 0.9);// modrá barva
// vykreslení vrcholu koule
glVertex3d(R * cos(UHEL(0)) * sin(UHEL(0)), R * cos(UHEL(0)), R * sin(UHEL(0)) * sin(UHEL(0)));
}
else// nad hladinou moře
{
// barva mezi zelenou a hnědou (podle nadmořské výšky)
glColor3d(0.455 * (m_r[0][0]-R) / (m_max_r-R), 0.39 * (m_r[0][0]-R) / (m_max_r-R) + (1.0 - (m_r[0][0] - R) / (m_max_r-R)), 0.196 * ((m_r[0][0] - R) / (m_max_r - R)));
// vykreslení vrcholu koule
glVertex3d(m_r[0][0] * cos(UHEL(0)) * sin(UHEL(0)), m_r[0][0] * cos(UHEL(0)), m_r[0][0] * sin(UHEL(0)) * sin(UHEL(0)));
}
for(i=0; i<SLICES; i++)
for(j=0; j<SLICES/2; j++)
{
if (m_r[i][(j + 1) % (SLICES / 2)] <= R)// pod hladinou moře
{
glColor3d(0, 0, 0.9);// modrá barva
// vykreslení vrcholu koule
glVertex3d(R * cos(UHEL(i)) * sin(UHEL(j + 1)), R * cos(UHEL(j + 1)), R * sin(UHEL(i)) * sin(UHEL(j + 1)));
}
else
{
// barva mezi zelenou a hnědou (podle nadmořské výšky)
glColor3d(0.455 * ((m_r[i][(j + 1) % (SLICES/2)] - R) / (m_max_r - R)), 0.39 * (m_r[i][(j + 1) % (SLICES / 2)] - R) / (m_max_r - R) + (1.0 - (m_r[i][(j + 1) % (SLICES / 2)] - R) / (m_max_r - R)), 0.196 * ((m_r[i][(j + 1) % (SLICES / 2)] - R) / (m_max_r - R)));
// vykreslení vrcholu koule
glVertex3d(m_r[i][(j + 1) % (SLICES / 2)] * cos(UHEL(i)) * sin(UHEL(j + 1)), m_r[i][(j + 1) % (SLICES / 2)] * cos(UHEL(j + 1)), m_r[i][(j + 1) % (SLICES / 2)] * sin(UHEL(i)) * sin(UHEL(j + 1)));
}
if (m_r[(i+1)%SLICES][j] <= R)// pod hladinou moře
{
glColor3d(0, 0, 0.9);// modrá barva
// vykreslení vrcholu koule
glVertex3d(R * cos(UHEL(i + 1)) * sin(UHEL(j)), R * cos(UHEL(j)), R * sin(UHEL(i + 1)) * sin(UHEL(j)));
}
else
{
// barva mezi zelenou a hnědou (podle nadmořské výšky)
glColor3d(0.455 * ((m_r[(i + 1) % SLICES][j] - R) / (m_max_r - R)), 0.39 * (m_r[(i + 1) % SLICES][j] - R) / (m_max_r - R) + (1.0 - (m_r[(i + 1) % SLICES][j] - R) / (m_max_r - R)), 0.196 * ((m_r[(i + 1) % SLICES][j] - R) / (m_max_r - R)));
// vykreslení vrcholu koule
glVertex3d(m_r[(i + 1) % SLICES][j] * cos(UHEL(i + 1)) * sin(UHEL(j)), m_r[(i + 1) % SLICES][j] * cos(UHEL(j)), m_r[(i + 1) % SLICES][j] * sin(UHEL(i + 1)) * sin(UHEL(j)));
}
}
glEnd();
}
Pro úplnost zde uvedu ještě výpis funkce Reset(), konstruktoru a destruktoru.
void CPlanet::Reset(const double r)
{
// všechny vrcholy se nastaví na výchozí poloměr
m_default_r=r;
register int i,j;
for(i=0; i<SLICES; i++)
for(j=0; j<SLICES/2; j++)
m_r[i][j]=R;
}
CPlanet::CPlanet()
{
Reset(20);
srand( (unsigned)time( NULL ) );
}
CPlanet::~CPlanet()
{
}
Náprava nedostatku
Výše uvedený nedostatek, tj. že tam, kde se na jedné straně planety vyskytuje kontinent je na druhé straně moře, lze obejít jednoduše tak, že kouli nerozdělujete středem, ale libovolným bodem, který do ní patří. Pro definování tohoto bodu se může použít normálový vektor plochy, jen musíme trochu upravit způsob jeho výpočtu - nestačí pouze jednotkový normálový vektor, ale musí se volit (o náhodné velikosti) menší než je poloměr koule.
nx = double(rand() % int(R)) * ((double(rand()) / double(RAND_MAX)) - 0.5);
ny = double(rand() % int(R)) * ((double(rand()) / double(RAND_MAX)) - 0.5);
nz = double(rand() % int(R)) * ((double(rand()) / double(RAND_MAX)) - 0.5);
Ještě je nutné modifikovat způsob výpočtu proměnné ns, tak aby se počítalo od bodu daného normálovým vektorem.
ns = nx * (x - nx) + ny * (y - ny) + nz * (z - nz);
Tím ale vznikne další problém. Protože normálový vektor ukazuje vždy od středu k dělící rovině, větší část koule se bude vždy zmenšovat. To lze ale odstranit následující jednoduchou úpravou podmínky rozhodující, zda zmenšovat nebo zvětšovat.
if (m * ns >= 0)// úhel mezi vektory menší nebo roven 90 stupňů
{
// zvýšit vrchol
m_r[i][j] += 1e-3 * R;
}
else// úhel mezi vektory větší než 90 stupňů
{
// snížit vrchol
m_r[i][j] -= 1e-3 * R;
}
Jediný rozdíl od předcházejícího kódu je v násobení proměnnou m, která má hodnotu buď plus nebo mínus jedna (náhodně). Tuto hodnotu volíme vždy pouze jednou pro každý výpočet normálového vektoru. Nejlepší je umístit následující řádek hned za výpočet proměnných nx, ny, nz.
m = ((rand() % 2) ? -1 : 1)
Výsledek upraveného algoritmu bude vypadat například takto:


... mezi přední a zadní stranou už není žádná shoda.
napsal: Milan Turek <nalim.kerut (zavináč) email.cz>
Anglický originál
Zdrojové kódy
- 29.6 kB - Ukázkové demo ve Visual C++