Analytická geometrie
Tento článek vychází z mých zápisků do matematiky z druhého ročníku na střední škole. Jo, na diktování byla Wakuovka vždycky dobrá... Tehdy jsem moc nechápal k čemu mi tento obor matematiky vůbec bude, ale když jsem se začal věnovat OpenGL, záhy jsem pochopil. Zkuste si vzít například nějaký pozdější NeHe Tutoriál. Bez znalostí 3D matematiky nemáte šanci. Doufám, že vám tento článek pomůže alespoň se základy a pochopením principů.
Kartézská soustava souřadnic
Tak tedy začneme. Co je geometrie ví snad každý. Ale co je analytická geometrie? Dala by se definovat velice jednoduše: Analytická geometrie řeší výpočtem to, co se dá nakreslit. A přesně o to se v počítačové grafice jedná. Pro všechny výpočty je nutná soustava souřadnic. Tvoří ji dvě (popř. tři) navzájem kolmé osy, které mají stejně velké jednotky.
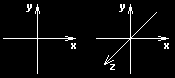
Bod
Nejjednodušším útvarem je bod. Nemá žádný rozměr, ale pouze polohu. Jeho poloha má ve dvourozměrném systému dvě složky, ve třírozměrném tři atd. Formálně se zapisuje takto: JMÉNO BODU[x, y]. V následujícím příkladu by se uvedené body definovaly takto:
A[-2; 1]
B[ 3; 1]
C[-2; 3]
S[ ?; ?]// Je středem úsečky BC
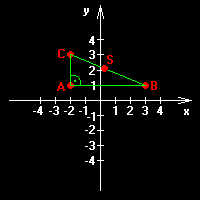
Střed úsečky - grafická metoda
Bod S jsme nedefinovali, protože jen tak od oka jeho složky neurčíme. Víme pouze, že je středem úsečky BC a chceme určit polohu. V případě grafické metody bychom si vzali papír, tužku a pravítko, nakreslili bychom souřadnicové osy, vepsali body a spojili je úsečkami. Dále bychom změřili délku úsečky BC, vydělili ji dvěma a tuto vypočítanou vzdálenost nanesli (je jedno, zda z bodu B nebo C, protože S je v polovině). Odečteme jednotlivé x, y složky a získáme polohu bodu S.
Střed úsečky - početní metoda
Jiná je ale situace, kdybychom neměli žádné pomůcky a museli všechno spočítat. Z obrázku jde na první pohled vidět, že x-ová složka bodu S je průměrem x-ových složek bodu B a C. Y-ová složka je to samé. Můžeme tedy vytvořit vzorec a dosadit hodnoty. Porovnáme-li výsledek S[0,5; 2] s obrázkem, souřadnice odpovídají. Od nynějška budeme používat pouze početní metodu.
S[x; y] = [((xB + xC) / 2); ((yB + yC) / 2)]
S[((3 - 2)) / 2); ((1 + 3) / 2)]
S[0,5; 2]
Délka úsečky
Druhým problémem může být, pokud chceme zjistit délku úsečky BC. Opět se podíváme na obrázek a na první pohled vidíme :-), že úsečka BC je přeponou pravoúhlého trojúhelníku ABC, pro který platí Pythagorova věta.
c2 = a2 + b2
c = sqrt(a2 + b2)// sqrt(x) = druhá odmocnina z x
Dá se říct, že následující vzorec by platil i tehdy, pokud by trojúhelník ABC nebyl pravoúhlý a dokonce i tehdy, pokud bychom neměli vůbec žádný trojúhelník, ale pouze úsečku BC. Pravým úhlem je v tomto případě kolmost souřadnicových os, délky stran a, c zastupují průměty úsečky do os x, y. Pythagorova věta tedy stále platí.
|BC| = sqrt((xB - xC)2 + (yB - yC)2)
|BC| = sqrt(52 + (-2)2)
|BC| = sqrt(25 + 4)
|BC| = sqrt(29)
|BC| = 5,3851
Vektor
Vektory obecně určují, jak se změní složky souřadnic x a y než se přesuneme z počátku vektoru na jeho konec. Značí se šipkou směřující zleva doprava (od počátečního do koncového bodu) nad jménem vektoru. Pozn.: V tomto článku ho značím pouze čárou, protože nemohu přijít na to, jak v HTML vytvořit šipku. Narozdíl od bodu, který se umísťuje do hranatých, píšeme složky vektoru do obyčejných kulatých závorek. Chceme-li zjistit vektor BC odečteme od koncového bodu, počátek.
BC = ((xC - xB); (yC - yB))
BC = ((-2 -3); (3-1))
BC = (-5; 2)
Dva stejné vektory (stejně velké a stejně orientované) představují v matematice dvě různá umístění téhož vektoru. Z toho plyne, že vektor můžeme přenést kamkoli na rovnoběžnou přímku, akorát nesmíme změnit jeho velikost. Toto ale neplatí ve fyzice, kde se u vektoru, kromě velikosti musí určit i počátek nebo konec (např. působiště síly).
Velikost vektoru
Při zjišťování velikosti vektoru se postupuje úplně stejně jako při určování délky úsečky.

|AB| = sqrt((xB - xA)2 + (yB - yA)2)
Normalizace vektoru na jednotkovou délku
V matematice není u vektoru důležitá jeho délka, ale směr. Směřují-li dva vektory stejným směrem, jsou shodné (mohou ležet i na libovolných rovnoběžkách). Jednotkovou délku vektoru vypočítáme tak, že získáme aktuální délku vektoru a touto hodnotou vydělíme jednotlivé x, y, z složky.
Počítání s vektory
Sčítání a odečítání
Vždy sečteme zvlášť x-ové a zvlášť y-složky. Nic těžkého.
a = (-3; 2)
b = ( 4; 6)
a + b = ( 1; 8)
a - b = (-7;-4)
Násobení a dělení vektoru číslem
Opět vynásobíme zvlášť jednotlivé složky.
4 * a = (4 * xa; 4 * ya)
4 * a = (-12; 8)
Skalární součin vektorů
Násobí se zvlášť x-ové a zvlášť y-ové složky, které se sečtou.
u * v = uX*vX + uY*vY
Nebo také
u * v = |u| * |v| * cos uhel
Úhel dvou vektorů
Ze vzorce pro výpočet skalárního součinu vektorů (viz. výše) lze odvodit vztah pro výpočet úhlu dvou vektorů.
cos uhel = (u * v) / (|u| * |v|)
Dosadíme-li do rovnice dříve uvedené vzorce, získáme následující vztah:
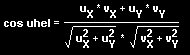
A pokud budou vektory normalizované (jednotková délka), můžeme jmenovatel ze zlomku vypustit, protože se rovná jedné.
cos uhel = (u * v)// Za předpokladu jednotkových délek
Vektorový součin dvou vektorů
Vynásobíme-li vektorově dva vektory, získáme vektor třetí, který je kolmý k rovině určené původními dvěma vektory. Aby bylo možno určit vektorový součin, nesmí být vektory u a v rovnoběžné, protože by netvořily rovinu. Vektorový součin se neznačí operátorem *, ale x.
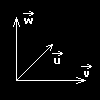
u = (-3; 5; -1)
v = ( 1; 2; -4)
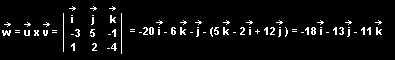
Nyní položíme vektory i, j, k rovny jedné (jednotkové vektory). Násobením jedničkou se koeficienty nezmění, takže jsme právě získali výsledek.
w = (-18; -13; -11)
Vektorové prostory
Lineárně závislé a lineárně nezávislé vektory
Dimenze (rozměr) vektorového prostoru určuje maximální počet lineárně nezávislých vektorů. Je také dána počtem složek souřadnice. Vektory jsou lineárně závislé, když pro libovolný vektor soustavy vektorů platí:
v1, v2, v3 ... vn
vm = k1*v1 + k2*v2 + ... + kn*vn
Pro lineárně nezávislé vektory tato rovnice neplatí pro žádný vektor systému.
Jednorozměrný prostor - přímka
Jednorozměrný prostor má pouze jeden nezávislý vektor. Ostatní vektory na přímce se dají pomocí tohoto vektoru vyjádřit.

Dvourozměrný prostor - rovina
Má dva lineárně nezávislé vektory.
Třírozměrný prostor
Má tři lineárně nezávislé vektory. Myslím, že podstatu už chápete. Tyto vlastnosti se využívají k řešení systému N rovnic o N neznámých.
Kolmé vektory
Dva kolmé vektory v rovině mají obrácené pořadí složek a u jedné z nich (jedno které) opačné znaménko. Kolmý vektor k zadanému vektoru je rovněž libovolný k-násobek vektoru získaného uvedeným postupem. Odvození této definice vychází ze vzorce pro úhel dvou vektorů, kde se za úhel dosadí 90°.
a = ( 3; 2)
b = ( ?; ?)// Je kolmý k a
b = ( 2;-3)
b = (-2; 3)
b = (-4; 6)// Atd.
Rovnice přímky v rovině
Typy rovnic přímky:
- Parametrické rovnice přímky
- Obecný tvar
- Směrnicový tvar
- Směrnicový tvar určený souřadnicemi bodů
- Úsekový tvar
Parametrický tvar rovnic přímky
Následující vzorec je parametrickou rovnicí přímky.
p:
x = AX + sX*t
y = AY + sY*t

A[2; 4]
s = (5; 7)
p:
x = 2 + 5*t
y = 4 + 7*t
Sestavení parametrických rovnic ze dvou bodů
Toto už by mělo být jasné, ale myslím si, že malá ukázka škodit nebude. Je úplně jedno, zda po získání vektoru dosadíme do rovnice souřadnice bodu A nebo B, protože oba leží na hledané přímce.
A[2; 4]
B[5; 3]
s = B - A = (5-2; 3-4) = (3; -1)
p:
x = 2 + 3*t
y = 4 - t
A ještě si zkusíme, zda bod C[1; 2] na této přímce leží nebo ne. Za x a y dosadíme jeho souřadnice a pokud se budou parametry t v obou rovnicích rovnat, C leží na přímce.
p:
1 = 2 + 3*t => 3*t = -1 => t = -1/3
2 = 4 - t => -t = -2 => t = 2
V první rovnici vyšlo t rovno -1/3 v druhé se t rovnalo 2. Z toho plyne, že bod C neleží na přímce t.
Nevýhoda parametrického vyjádření je v tom, že na první pohled nepoznáme, jestli se jedná u dvou soustav rovnic o tutéž přímku nebo ne.
Počítání s rovnicemi přímek v parametrickém tvaru
Předem se omlouvám za to, ale všechno bude pouze teoreticky, protože psaní příkladů v HTML mi už leze opravdu na nervy.
Rovnici přímky sestavit umíme, ale jak bychom postupovali při hledání rovnice přímky, která je rovnoběžná ke známé přímce v určitém bodě? Vycházíme z toho, že rovnoběžné přímky mohou mít stejné směrové vektory, takže pouze nahradíme souřadnice bodu v rovnicích.
U kolmé přímky by se opět nahradily souřadnice bodu, ale navíc bychom ještě museli změnit vektor na kolmý - nic těžkého (viz. kolmé vektory).
Průsečík dvou přímek je společným řešením dvou rovnic přímek. V parametrickém tvaru porovnáme souř. x první přímky se souř. x druhé přímky. Vypočteme parametr t a jestli platí rovnost i pro souřadnice y při stejném t, je tento parametr příslušný k průsečíku. Dosazením parametru do rovnic dostaneme souřadnice průsečíku.
Úhel dvou přímek je úhlem mezi dvěma směrovými vektory (viz. Úhel dvou vektorů).
Obecná rovnice přímky
Níže je uveden její vzorec. Proměnné x a y jsou souřadnice bodu, který leží na přímce. A, b jsou složky normálového vektoru přímky.
p: a*x + b*y + c = 0

Sestavení obecné rovnice přímky ze dvou bodů
Nejprve vypočítáme směrový vektor a ten převedeme na normálový. Tím získáme proměnné a, b, x, y. Zůstane nám jednoduchá rovnice o jedné neznámé. Vypočteme c a dosadíme do původní rovnice
A[2; 4]
B[5; 3]
s = AB = (5-2; 3-4) = (3; -1)// Směrový vektor
n = (1; 3)// Normálový vektor
Získali jsme čísla a = 1, b = 3 a použijeme např. složky bodu A (je to jedno). Vše dosadíme do rovnice přímky a hledáme číslo c.
p: a*x + b*y + c = 0
p: 1*2 + 3*4 + c = 0
c = - (1*2 + 3*4) = - (2 + 12) = -14
Nakonec dosadíme do rovnice přímky čísla a, b, c a máme výsledek.
p: x + 3y - 14 = 0// Výsledná rovnice přímky
Ještě jedna poznámka na konec. Je-li směrový (popř. normálový) vektor zadán tak, že jeho složky se dají rozšířit nebo krátit, můžeme za něj zvolit jeho libovolný k násobek. Následující dvě rovnice přímek jsou tedy totožné:
p: -4x + 8y + 24 = 0
p: -x + 2y + 6 = 0// Vykrácená verze
Rovnice rovnoběžných přímek
Hledáme rovnoběžku q s přímkou p: x - 2y + 3 = 0, která prochází bodem M[2; 5]. Stačí dosadit souřadnice bodu M do rovnice p a vypočítat číslo c, které dosadíme do původní rovnice p. Všimněte si, že se přímky liší pouze číslem c.
q: x - 2y + c = 0
2 - 2*5 + c = 0
c = 8
q: x - 2y + 8 = 0// Přímka q je rovnoběžná s p
p: x - 2y + 3 = 0
Rovnice kolmých přímek
Opět pouze postup: Vytvoří se kolmý vektor k normálovému vektoru původní přímky. Spolu s bodem, kterým má kolmá přímka procházet, se dosadí do rovnice a vypočítá se c. Příklad dvou kolmých přímek:
p: 5x - 6y + 4 = 0
q: 6x + 5y -15 = 0
Stejně jako rovnoběžné přímky, jsou si také trochu podobné...
Rovnice přímky ve směrnicovém tvaru
Směrnicový tvar rovnice přímky se užívá tam, kde je zadán sklon přímky vzhledem k ose x nebo je-li směrnice vypočtena jiným způsobem (např. derivací). Číslo q v následující rovnici označuje úsek na ose y, kde ji přímka protíná. K je směrnice přímky, která se vypočítá goniometrickou funkcí k = tg a. Je to také derivace jakékoli funkce - tedy tečna k jejímu grafu.
y = k*x + q
Nebo také:
y - yA = k * (x - xA)

Získání čísla k
Vycházíme z toho, že k = tg a. Postup zjištění tg a vysvětluje obrázek.

Po zjištění čísla k nám už nic nebrání tomu, abychom ho spolu se složkami bodu A nebo B dosadili do rovnice a získali q.
Rovnoběžky a kolmice
Rovnoběžné přímky mají v rovnicích stejnou hodnotu k, liší se v q. Kolmice mají v k zápornou převrácenou hodnotu. To znamená, že pokud je u jedné například k = 2, u druhé bude k = - 1/2.
Vzdálenost bodu od přímky a vzdálenost dvou rovnoběžek
Čísla a, b, c jsou konstanty z rovnice přímky v obecném tvaru a čísla x, y jsou souřadnice bodu. Stačí pak dosadit do vzorce.
Vzdálenost dvou rovnoběžek lze zjistit úplně stejně. Nejdříve získáme bod, který leží na jedné z nich a pak opět dosadíme do vzorce.
Rovina v prostoru
Typy rovnic rovin:
- Parametrické rovnice roviny
- Obecná rovnice
Parametrické rovnice roviny
Jsou skoro stejné jako parametrické rovnice přímky. Následuje vzorec a příklad.
R:
x = AX + kX*u + lX*v
y = AY + kY*u + lZ*v
z = AZ + kY*u + lZ*v
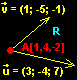
R:
x = 1 + 3k +l
y = 4 - 4k - 5l
z = -2 + 7k - l
Obecná rovnice roviny
Vzorec je analogický vzorci obecné rovnice přímky. Čísla a, b, c jsou složky normálového vektoru roviny a čísla x, y, z jsou souřadnice bodu, který na ní leží. Stejně jako se u přímky dopočítávalo c, nyní se musí spočítat d - žádný problém, vše už známe.
R: ax + by + cz + d = 0
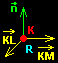
Dáme si jeden příklad a zároveň ho teoreticky! vyřešíme. Určete rovnici roviny R, která je dána body K[-2; 1; 1], L[0; 3; -5]; M[4; -6; 9]. Postupujeme tak, že určíme jeden bod jako základní, například K a určíme vektory KL a KM. Potřebujeme určit vektor, který je kolmý k oběma najednou. Získáme ho vektorovým součinem vektorů n = KL x KM. Výsledek dosadíme do rovnice roviny a vypočítáme neznámou d.
Zvláštní polohy roviny v prostoru
Rovina procházející počátkem souřadnic
Jeden bod v rovině (počátek souřadnic) má souřadnice 0[0; 0; 0]. Z toho plyne, že:
R: a*x + b*y + c*z + d = 0
R: a*0 + b*0 + c*0 + d = 0
d = 0// Výsledná rovnice roviny
Rovina rovnoběžná s některou osou
Chybí koeficient u proměnné, která patří ke konkrétní ose.
R: 3y - 2z + 5 = 0// Rovina rovnoběžná s osou x
Rovina rovnoběžná s dvěma osami
U obou chybí koeficienty a třetí složka je konstantní.
R: 3z + 5 = 0// Rovina rovnoběžná s osami x a y
z = - 5/3
z = konst.
Způsoby zadání roviny
Každá rovina je zadána vždy třemi nezávislými prvky:
- Tři body neležící v přímce
- Dvě přímky, které nejsou mimoběžné (= které se protínají)
- Jeden bod a dva směrové vektory
- Rovnoběžnost roviny s některou osou a dva body, popř. jedna přímka
- Rovnoběžnost roviny se dvěma osami a jeden bod
Přímka v prostoru
V rovině mohla být přímka vyjádřena mnoha způsoby, které se v prostoru smrskly na jediný možný způsob - parametrické rovnice.
Parametrická rovnice přímky
Tohle už známe, takže to nebudu zbytečně rozepisovat, přidává se pouze další rovnice pro osu z.
p:
x = AX + sX*t
y = AY + sY*t
z = AZ + sZ*t
Hledáme-li přímku jako průsečnici dvou rovin, zvolíme dva body, které leží současně v obou rovinách - tj. jednu souřadnici zvolíme a ostatní dvě musí vyhovovat rovnicím obou rovin. Pak stačí vytvořit směrový vektor a následně ho s jedním z bodů dosadit do parametrických rovin přímek.
Závěr
... a nyní byste měli rozumět alespoň základům analytické geometrie. My jsme toto učivo brali ve škole skoro čtvrt roku, takže tento článek berte jako stručný!!! výtah. Pokud se vám zdá, že je vše jakoby useknuté, máte pravdu. Jak to tak bývá, skončil školní rok a na začátku dalšího už se nepokračovalo. Také musím poznamenat, že ke každého tématu máme v sešitě několik příkladů, ale opisovat je sem by se s největší pravděpodobností stalo mojí noční můrou - děkuji za pochopení... nebo jinak řečeno: Buďte rádi za to, co tady máte, psal jsem to skoro týden, čtyři hodiny denně :-)
napsal: Michal Turek - Woq <WOQ (zavináč) seznam.cz>