Přímka ve 2D
Radomír Vrána mě požádal o radu, jak vypočítat průsečík dvou 2D přímek. Rozhodl jsem se, že mu místo obecných matematických vzorců pošlu rovnou kompletní C++ kód. Nicméně mi trochu přerostl přes hlavu, a tak vznikla kompletní třída přímky v obecném tvaru. Kromě průsečíku umí určit i jejich vzájemnou polohu (rovnoběžné, kolmé...), úhel, který svírají nebo vzdálenost libovolného bodu od přímky. Doufám, že tento můj drobný úlet nebude moc vadit :-]
Kód rozdělíme klasicky na hlavičkový a implementační soubor třídy, začneme hlavičkovým. Aby nenastaly problémy při vícenásobném inkludování, nadefinujeme symbolickou konstantu __PRIMKA2D_H__ a před vlastní definicí otestujeme, jestli už existuje. Pokud ano, instrukce preprocesoru #ifndef zajistí, že se tento soubor nebude zpracovávat dvakrát.
#ifndef __PRIMKA2D_H__
#define __PRIMKA2D_H__
#include <math.h>// Matematická knihovna
Předpokládám, že už znáte rovnici přímky v obecném tvaru, ale pro ty z vás, kteří ještě nejsou na střední škole (konec druhého ročníku), ji zkusím alespoň naznačit.
Obecná rovnice přímky je vyjádřena ve tvaru a*x + b*y + c = 0. Pokud za x, y dosadíme souřadnice libovolného 2D bodu a vyjde nám nula, máme jistotu, že tento bod na přímce leží. Konstanty a, b představují normálový vektor přímky (vektor, který je k přímce kolmý). c je také konstanta, určí se výpočtem při dosazení bodu do rovnice. Kromě obecného tvaru existují i další vzájemně zaměnitelné tvary - například parametrický a směrnicový.
Myslím, že komentáře vše vysvětlují...
class WPrimka2D// Třída 2D přímky v obecném tvaru
{
private:
double a, b, c;// Obecná rovnice přímky a*x + b*y + c = 0
public:
WPrimka2D();// Konstruktor
~WPrimka2D();// Destruktor
WPrimka2D(const WPrimka2D& primka);// Kopírovací konstruktor
WPrimka2D(double a, double b, double c);// Přímé zadání proměnných
WPrimka2D(double x1, double y1, double x2, double y2);// Přímka ze dvou bodů
void Create(double a, double b, double c);// Přímé zadání proměnných
void Create(double x1, double y1, double x2, double y2);// Přímka ze dvou bodů
inline double GetA() { return a; }// Získání atributů
inline double GetB() { return b; }
inline double GetC() { return b; }
bool operator==(WPrimka2D& primka);// Splývající přímky?
bool operator!=(WPrimka2D& primka);// Nesplývající přímky?
bool JeNaPrimce(double x, double y);// Leží bod na přímce?
bool JsouRovnobezne(WPrimka2D& primka);// Jsou přímky rovnoběžné?
bool JsouKolme(WPrimka2D& primka);// Jsou přímky kolmé?
bool Prusecik(WPrimka2D& primka, double& retx, double& rety);// Průsečík přímek
double Uhel(WPrimka2D& primka);// Úhel přímek (v radiánech)
double VzdalenostBodu(double x, double y);// Vzdálenost bodu od přímky
};
#endif
Hlavičkový soubor je za námi. Začneme implementovat jednotlivé metody. V obecném konstruktoru nastavíme všechny vlastnosti na nulu, destruktor necháme prázdný.
#include "primka2d.h"// Hlavičkový soubor
WPrimka2D::WPrimka2D()// Obecný konstruktor
{
a = 0.0;// Nulování
b = 0.0;
c = 0.0;
}
WPrimka2D::~WPrimka2D()// Destruktor
{
}
Kopírovací konstruktor...
WPrimka2D::WPrimka2D(const WPrimka2D& primka)// Kopírovací konstruktor
{
a = primka.a;
b = primka.b;
c = primka.c;
}
Abychom mohli inicializovat třídu už při jejím vytvoření, přetížíme konstruktor. Kdykoli v programu ho může nahradit metoda Create().
WPrimka2D::WPrimka2D(double a, double b, double c)// Přímé zadání proměnných
{
Create(a, b, c);
}
void WPrimka2D::Create(double a, double b, double c)// Přímé zadání proměnných
{
this->a = a;
this->b = b;
this->c = c;
}
Čtvrtý konstruktor umí vytvořit přímku ze dvou bodů, opět ho může nahradit funkce Create(). Jak jsem naznačil výše, proměnné a, b představují normálový vektor přímky. Směrový vektor by se získal jednoduchým odečtením koncového bodu od počátečního. Vytvoření normálového vektoru je podobné, ale navíc prohodíme složky vektoru a u jedné invertujeme znaménko.
Raději příklad. Máme dva body [1; 2] a [4; 3], směrový vektor se získá odečtením koncového bodu od počátečního, nicméně při vytváření přímky je úplně jedno, který považujeme za počáteční a který za koncový. První bod bude například počáteční a druhý koncový. Směrový vektor je tedy s = (4-1, 3-2) = (3; 1). Normálový vektor má prohozené pořadí složek a u jedné opačné znaménko. n = (-1; 3) nebo (1; -3).
Pro úplnost: je naprosto jedno, zda vezmeme přímo vypočtený vektor nebo jeho k-násobek. Oba vektory uvedené v minulém odstavci jsou k-násobkem toho druhého (k = -1). Stejně tak bychom mohli vykrátit vektor (5; 10) na (1; 2). Z toho plyne, že jedna přímka může být k-násobkem druhé - viz. dále.
WPrimka2D::WPrimka2D(double x1, double y1, double x2, double y2)// Přímka ze dvou bodů
{
Create(x1, y1, x2, y2);
}
void WPrimka2D::Create(double x1, double y1, double x2, double y2)
{
if(x1 == x2 && y1 == y2)// 2 stejné body netvoří přímku
{
Create(0.0, 0.0, 0.0);// Platné hodnoty
return;
}
a = y2 - y1;
b = x1 - x2;
Proměnnou c vypočteme dosazením jednoho bodu (v našem případě prvního) do zatím neúplné rovnice. V základní rovnici a*x + b*y + c = 0 přesuneme všechno kromě c na pravou stranu a získáme c = -a*x -b*y.
c = -a*x1 -b*y1;
}
Zda bod leží na přímce, zjistíme dosazením jeho souřadnic do rovnice přímky. Pokud se výsledek rovná nule, leží na ní.
bool WPrimka2D::JeNaPrimce(double x, double y)// Leží bod na přímce?
{
if(a*x + b*y + c == 0.0)// Dosazení souřadnic do rovnice
{
return true;
}
else
{
return false;
}
}
Jestli jsou přímky stejné (splývající) se zjistí porovnáním jejich složek, ale navíc musíme vzít v úvahu i k-násobky. Nebudeme tedy porovnávat přímo vnitřní proměnné, ale místo toho vypočteme poměry a/a, b/b a c/c. Budou-li tyto poměry vnitřních proměnných stejné, je jasné, že se jedná se o jednu a tu samou přímku.
bool WPrimka2D::operator==(WPrimka2D& primka)// Jsou přímky splývající?
{
double ka = a / primka.a;// Nestačí pouze zkontrolovat hodnoty, primka může být k-násobkem
double kb = b / primka.b;
double kc = c / primka.c;
if(ka == kb && ka == kc)// Musí být stejné
{
return true;// Splývající přímky
}
else
{
return false;// Dvě různé přímky
}
}
bool WPrimka2D::operator!=(WPrimka2D& primka)// Nejsou přímky splývající?
{
return !(*this == primka);// Negace porovnání
}
Zjištění, jestli jsou přímky rovnoběžné, je velmi podobné operátoru porovnání. Mají-li stejný normálový vektor, popř. vektor jedné je k-násobkem druhé, jsou rovnoběžné. Třetí proměnnou, c, nemusíme a vlastně ani nesmíme testovat.
bool WPrimka2D::JsouRovnobezne(WPrimka2D& primka)// Jsou přímky rovnoběžné?
{
double ka = a / primka.a;// Nestačí zkontrolovat hodnoty, p může být k-násobkem
double kb = b / primka.b;
if(ka == kb)// Musí být stejné
{
return true;
}
else
{
return false;
}
}
Kolmost dvou přímek se nejjednodušeji odhalí tak, že se jedna z nich natočí o 90 stupňů a otestuje se jejich rovnoběžnost - proč to zbytečně komplikovat...
bool WPrimka2D::JsouKolme(WPrimka2D& primka)// Jsou přímky kolmé?
{
WPrimka2D pom(-primka.b, primka.a, primka.c);// Přímka s kolmým vektorem
return JsouRovnobezne(pom);
}
Dostáváme se k podstatě celého článku - průsečík dvou přímek. Nejdříve otestujeme jestli se nejedná o dvě splývající přímky, pokud ano, mají nekonečně mnoho společných bodů. Nejsou-li splývající, mohou být ještě rovnoběžné, pak nemají žádný společný bod. Ve všech ostatních případech mají pouze jeden společný bod a tím je průsečík. Protože musí vyhovovat současně oběma rovnicím, řešíme soustavu dvou rovnic o dvou neznámých x a y.
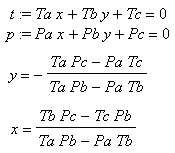
Pokud funkce vrátí true, byl průsečík nalezen, souřadnice uložíme do referencí retx a rety. False indikuje buď žádný průsečík (rovnoběžné přímky), nebo nekonečně mnoho společných bodů (splývající přímky).
bool WPrimka2D::Prusecik(WPrimka2D& primka, double& retx, double& rety)// Průsečík přímek
{
if(*this == primka)// Přímky jsou splývající - nekonečně mnoho společných bodů
{
return false;// Spíše by se mělo vrátit true a nějaký bod... záleží na použití
}
else if(JsouRovnobezne(primka))// Přímky jsou rovnoběžné - žádný společný bod
{
return false;
}
else// Jeden společný bod - průsečík (vyhovuje současně oběma rovnicím)
{
retx = (b*primka.c - c * primka.b) / (a*primka.b - primka.a*b);
rety = -(a*primka.c - primka.a * c) / (a*primka.b - primka.a*b);
return true;
}
}
Úhel dvou přímek je úhlem dvou směrových vektorů, můžeme však použít i normálové vektory, protože výsledek bude stejný. Kosinus úhlu se rovná zlomku, u kterého se v čitateli nachází skalární součin vektorů (násobí se zvlášť x a zvlášť y složky) a ve jmenovateli součin délek vektorů (Pythagorova věta). Pokud nechápete, berte to jako vzorec.
double WPrimka2D::Uhel(WPrimka2D& primka)// Úhel přímek
{
return acos((a*primka.a + b*primka.b) / (sqrt(a*a + b*b) * sqrt(primka.a*primka.a + primka.b*primka.b)));
}
Vzdálenost bodu od přímky je už trochu složitější. Vypočte se rovnice přímky, která je kolmá k zadané přímce a prochází určeným bodem. Potom se najde průsečík těchto přímek a vypočte se vzdálenost bodů. Celý tento postup se ale dá mnohonásobně zjednodušit, když si najdete vzorec v matematicko fyzikálních tabulkách :-)
double WPrimka2D::VzdalenostBodu(double x, double y)// Vzdálenost bodu od přímky
{
double vzdalenost = (a*x + b*y + c) / sqrt(a*a + b*b);
if(vzdalenost < 0.0)// Absolutní hodnota
{
vzdalenost = -vzdalenost;
}
return vzdalenost;
}
Abych se ale vrátil na začátek, původním záměrem bylo vypočítat průsečík dvou přímek. S naší třídou to není nic složitého...
#include <stdio.h>// Knihovna pro standardní vstup a výstup
#include "primka2d.h"// Třída přímky
int main(int argc, char** argv)// Vstup do programu
{
WPrimka2D primka1(3.0, -1.0, 1.0);// Dvě přímky
WPrimka2D primka2(1.0, 3.0, -14.0);
double prusecik_x, prusecik_y;// Souřadnice průsečíku
if(primka1.Prusecik(primka2, prusecik_x, prusecik_y))// Výpočet průsečíku
{
printf("Průsečík [%f; %f]\n", prusecik_x, prusecik_y);// Vypsání hodnot
}
return 0;
}
Doufám, že se vám tento článek líbil. Pokud bude zájem (napište např. do Diskuze k tomuto článku), mohu vytvořit něco podobného o přímce ve 3D. Tam ale bode situace o trochu komplikovanější, protože v trojrozměrném prostoru obecná rovnice přímky neexistuje. Budeme si muset vystačit se soustavou parametrických rovnic.
napsal: Michal Turek - Woq <WOQ (zavináč) seznam.cz>
Zdrojové kódy
- 8.6 kB - Linuxové g++ OK, jiné kompilátory by měli být také použitelné