Lekce 28 - Bezierovy křivky a povrchy, fullscreen fix

David Nikdel je osoba stojící za tímto skvělým tutoriálem, ve kterém se naučíte, jak se vytvářejí Bezierovy křivky. Díky nim lze velice jednoduše zakřivit povrch a provádět jeho plynulou animaci pouhou modifikací několika kontrolních bodů. Aby byl výsledný povrch modelu ještě zajímavější, je na něj namapována textura. Tutoriál také eliminuje problémy s fullscreenem, kdy se po návratu do systému neobnovilo původní rozlišení obrazovky.

Tento tutoriál je od začátku zamýšlen pouze jako úvod do Bezierových křivek, aby někdo mnohem šikovnější než já dokázal vytvořit něco opravdu skvělého. Neberte ho jako kompletní Bezier knihovnu, ale spíše jako koncept, jak tyto křivky pracují a co dokáží. Také prosím omluvte mou, v některých případech, ne až tak správnou terminologii. Doufám, že bude alespoň trochu srozumitelná. Abych tak řekl: Nikdo není dokonalý...

Pochopit Bezierovy křivky s nulovými znalostmi matematiky je nemožné. Proto bude následovat maličko delší sekce teorie, která by vás měla do problematiky alespoň trochu zasvětit. Pokud všechno už znáte, nic vám nebrání tuto nut(d)nou sekci přeskočit a věnovat se kódu.

Bezierovy křivky bývají primární metodou, jak v grafických editorech či obyčejných programech vykreslovat zakřivené linky. Jsou obvykle reprezentovány sérií bodů, z nich každé dva reprezentují tečnu ke grafu funkce.

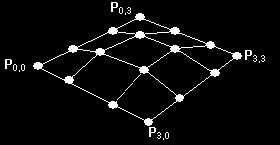
Toto je nejjednodušší možná Bezierova křivka. Delší jsou tvořeny spojením několika dohromady. Je tvořena pouze čtyřmi body, dva konce a dva středové kontrolní body. Pro počítač jsou všechny úplně stejné, ale abychom si pomohli, spojujeme první a poslední dva. Linky budou vždy tečnami k ukončovacím bodům. Parametrické křivky jsou kresleny nalezením libovolného počtu bodů rovnoměrně rozprostřených po křivce, které se spojí čárami. Počtem bodů můžeme ovládat hranatost křivky a samozřejmě také dobu trvání výpočtů. Podaří-li se nám množství bodů správně regulovat, pozorovatel v každém okamžiku uvidí perfektně zakřivený povrch bez trhání animace.

Všechny Bezierovy křivky jsou v založeny na základním vzorci funkce. Komplikovanější verze jsou z něj odvozeny.

t + (1 - t) = 1

Vypadá jednoduše? Ano, rovnice jednoduchá určitě je, ale nesmíme zapomenout na to, že je to pouze Bezierova křivka prvního stupně. Použijeme-li trochu terminologie: Bezierovy křivky jsou polynomiální (mnohočlenné). Jak si zajisté pamatujete z algebry, první stupeň z polynomu je přímka - nic zajímavého. Základní funkce vychází, dosadíme-li libovolné číslo t. Rovnici můžeme ovšem také mocnit na druhou, na třetí, na jakékoli číslo, protože se obě strany rovnají jedné. Zkusíme ji tedy umocnit na třetí.

(t + (1 - t))³ = 1³

t³ + 3t²(1 - t) + 3t(1 - t)² + (1 - t)³ = 1

Tuto rovnici použijeme k výpočtu mnohem více používanější křivky - Bezierovy křivky třetího stupně. Pro toto rozhodnutí existují dva důvody:

Tento polynomiál je nejnižšího možného stupně, kdy už křivka nemusí ležet v rovině, ale i v prostoru.
Tečny k funkci už nejsou závislé na jiných (křivky 2. stupně mohou mýt pouze tři kontrolní body, my potřebujeme čtyři).

Zbývá ale dodat ještě jedna věc... Celá levá strana rovnice se rovná jedné, takže je bezpečné předpokládat, že pokud přidáme všechny složky měla by se stále rovnat jedné. Zní to, jako by to mohlo být použito k rozhodnutí kolik z každého kontrolního bodu lze použít při výpočtu bodu na křivce? (nápověda: Prostě řekni ano ;-) Ano. Správně! Pokud chceme spočítat hodnotu bodu v procentech vzdálenosti na křivce, jednoduše násobíme každou složku kontrolním bodem (stejně jako vektor) a nalezneme součet. Obecně budeme pracovat s hodnotami 0 >= t >= 1, ale není to technicky nutné. Dokonale zmateni? Raději napíšu tu funkci.

P1*t³ + P2*3*t²*(1-t) + P3*3*t*(1-t)² + P4*(1-t)³ = P_new

Protože jsou polynomiály vždy spojité, jsou dobrou cestou k pohybu mezi čtyřmi body. Můžeme dosáhnout ale vždy pouze okrajových bodů (P1 a P4). Pokud tuto větu nechápete, podívejte se na první obrázek. V těchto případech se t = 0 popř. t = 1.

To je sice hezké, ale jak mám použít Bezierovy křivky ve 3D? Je to docela jednoduché. Potřebujeme 16 kontrolních bodů (4x4) a dvě proměnné t a v. Vytvoříme z nich čtyři paralelní křivky. Na každé z nich spočítáme jeden bod při určitém v a použijeme tyto čtyři body k vytvoření nové křivky a spočítáme t. Nalezením více bodů můžeme nakreslit triangle strip a tím zobrazit Bezierův povrch.

Přepokládám, že matematiky už bylo dost. Pojďme se vrhnout na kód této lekce. ( Ze všeho nejdříve vytvoříme struktury. POINT_3D je obyčejný bod ve třírozměrném prostoru. Druhá struktura je už trochu zajímavější - představuje Bezierův povrch. Anchors[4][4] je dvourozměrné pole 16 řídících bodů. Do display listu dlBPatch uložíme výsledný model a texture ukládá texturu, kterou na něj namapujeme.

typedef struct point_3d// Struktura bodu

{

double x, y, z;

} POINT_3D;

typedef struct bpatch// Struktura Bezierova povrchu

{

POINT_3D anchors[4][4];// Mřížka řídících bodů (4x4)

GLuint dlBPatch;// Display list

GLuint texture;// Textura

} BEZIER_PATCH;

Mybezier je objektem právě vytvořené textury, rotz kontroluje úhel natočení scény. ShowCPoints indikuje, jestli vykreslujeme mřížku mezi řídícími body nebo ne. Divs určuje hladkost (hranatost) výsledného povrchu.

BEZIER_PATCH mybezier;// Bezierův povrch

GLfloat rotz = 0.0f;// Rotace na ose z

BOOL showCPoints = TRUE;// Flag pro zobrazení mřížky mezi kontrolními body

int divs = 7;// Počet interpolací (množství vykreslovaných polygonů)

Jestli si pamatujete, tak v úvodu jsem psal, že budeme maličko upravovat kód pro vytváření okna tak, aby se při návratu z fullscreenu obnovilo původní rozlišení obrazovky (některé grafické karty s tím mají problémy). DMsaved ukládá původní nastavení monitoru před vstupem do fullscreenu.

DEVMODE DMsaved;// Ukládá původní nastavení monitoru

Následuje několik pomocných funkcí pro jednoduchou vektorovou matematiku. Sčítání, násobení a vytváření 3D bodů. Nic složitého.

POINT_3D pointAdd(POINT_3D p, POINT_3D q)// Sčítání dvou bodů

{

p.x += q.x;

p.y += q.y;

p.z += q.z;

return p;

}

POINT_3D pointTimes(double c, POINT_3D p)// Násobení bodu konstantou

{

p.x *= c;

p.y *= c;

p.z *= c;

return p;

}

POINT_3D makePoint(double a, double b, double c)// Vytvoření bodu ze tří čísel

{

POINT_3D p;

p.x = a;

p.y = b;

p.z = c;

return p;

}

Funkcí Bernstein() počítáme bod, který leží na Bezierově křivce. V parametrech jí předáváme proměnnou u, která specifikuje procentuální vzdálenost bodu od okraje křivky vzhledem k její délce a pole čtyř bodů, které jednoznačně definují křivku. Vícenásobným voláním a krokováním u vždy o stejný přírůstek můžeme získat aproximaci křivky.

POINT_3D Bernstein(float u, POINT_3D *p)// Spočítá souřadnice bodu ležícího na křivce

{

POINT_3D a, b, c, d, r;// Pomocné proměnné

// Výpočet podle vzorce

a = pointTimes(pow(u,3), p[0]);

b = pointTimes(3 * pow(u,2) * (1-u), p[1]);

c = pointTimes(3 * u * pow((1-u), 2), p[2]);

d = pointTimes(pow((1-u), 3), p[3]);

r = pointAdd(pointAdd(a, b), pointAdd(c, d));// Sečtení násobků a, b, c, d

return r;// Vrácení výsledného bodu

}

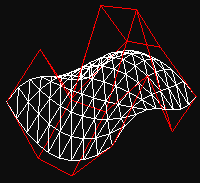
Největší část práce odvádí funkce genBezier(). Spočítá křivky, vygeneruje triangle strip a výsledek uloží do display listu. Použití display listu je v tomto případě více než vhodné, protože nemusíme provádět složité výpočty při každém framu, ale pouze při změnách vyžádaných uživatelem. Odstraní se tím zbytečné zatížení procesoru. Funkci předáváme strukturu BEZIER_PATCH, v níž jsou uloženy všechny potřebné řídící body. Divs určuje kolikrát budeme provádět výpočty - ovládá hranatost výsledného modelu. Následující obrázky jsou získány přepnutím do režimu vykreslování linek místo polygonů (glPolygonMode(GL_FRONT_AND_BACK, GL_LINES)) a zakázáním textur. Jasně je vidět, že čím je číslo v divs větší, tím je objekt zaoblenější.

GLuint genBezier(BEZIER_PATCH patch, int divs)// Generuje display list Bezierova povrchu

{

Proměnné u, v řídí cykly generující jednotlivé body na Bezierově křivce a py, px, pyold jsou jejich procentuální hodnoty, které slouží k určení místa na křivce. Nabývají hodnot v intervalu od 0 do 1, takže je můžeme bez komplikací použít i jako texturovací koordináty. Drawlist je display list, do kterého kreslíme výsledný povrch. Do temp uložíme čtyři body pro získání pomocné Bezierovy křivky. Dynamické pole last ukládá minulý řádek bodů, protože pro triangle strip potřebujeme dva řádky.

int u = 0, v;// Řídící proměnné

float py, px, pyold;// Procentuální hodnoty

GLuint drawlist = glGenLists(1);// Display list

POINT_3D temp[4];// Řídící body pomocné křivky

POINT_3D* last = (POINT_3D*) malloc(sizeof(POINT_3D) * (divs+1));// První řada polygonů

if (patch.dlBPatch != NULL)// Pokud existuje starý display list

glDeleteLists(patch.dlBPatch, 1);// Smažeme ho

temp[0] = patch.anchors[0][3];// První odvozená křivka (osa x)

temp[1] = patch.anchors[1][3];

temp[2] = patch.anchors[2][3];

temp[3] = patch.anchors[3][3];

for (v = 0; v <= divs; v++)// Vytvoří první řádek bodů

{

px = ((float)v) / ((float)divs);// Px je procentuální hodnota v

last[v] = Bernstein(px, temp);// Spočítá bod na křivce ve vzdálenosti px

}

glNewList(drawlist, GL_COMPILE);// Nový display list

glBindTexture(GL_TEXTURE_2D, patch.texture);// Zvolí texturu

Vnější cyklus prochází řádky a vnitřní jednotlivé sloupce. Nebo to může být i naopak. Záleží na tom, co si každý představí pod pojmy řádek a sloupec :-)

for (u = 1; u <= divs; u++)// Prochází body na křivce

{

py = ((float)u) / ((float)divs);// Py je procentuální hodnota u

pyold = ((float)u - 1.0f) / ((float)divs);// Pyold má hodnotu py při minulém průchodu cyklem

V každém prvku pole patch.anchors[] máme uloženy čtyři řídící body (dvourozměrné pole). Celé pole dohromady tvoří čtyři paralelní křivky, které si označíme jako řádky. Nyní spočítáme body, které jsou umístěny na všech čtyřech křivkách ve stejné vzdálenosti py a uložíme je do pole temp[], které představuje sloupec v řádku a celkově tvoří čtyři řídící body nové křivky pro sloupec.

Celou akci si představte jako trochu komplikovanější procházení dvourozměrného pole - vnější cyklus prochází řádky a vnitřní sloupce. Z upravených řídících proměnných si vybíráme pozice bodů a texturovací koordináty. Py s pyold představuje dva "rovněběžné" řádky a px sloupec. (Překl.: Než jsem tohle pochopil... v originále o tom nebyla ani zmínka).

temp[0] = Bernstein(py, patch.anchors[0]);// Spočítá Bezierovy body pro křivku

temp[1] = Bernstein(py, patch.anchors[1]);

temp[2] = Bernstein(py, patch.anchors[2]);

temp[3] = Bernstein(py, patch.anchors[3]);

glBegin(GL_TRIANGLE_STRIP);// Začátek kreslení triangle stripu

for (v = 0; v <= divs; v++)// Prochází body na křivce

{

px = ((float)v) / ((float)divs);// Px je procentuální hodnota v

glTexCoord2f(pyold, px);// Texturovací koordináty z minulého průchodu

glVertex3d(last[v].x, last[v].y, last[v].z);// Bod z minulého průchodu

Do pole last nyní uložíme nové hodnoty, které se při dalším průchodu cyklem stanou opět starými.

last[v] = Bernstein(px, temp);// Generuje nový bod

glTexCoord2f(py, px);// Nové texturové koordináty

glVertex3d(last[v].x, last[v].y, last[v].z);// Nový bod

}

glEnd();// Konec triangle stripu

}

glEndList();// Konec display listu

free(last);// Uvolní dynamické pole vertexů

return drawlist;// Vrátí právě vytvořený display list

}

Jediná věc, kterou neděláme, ale která by se určitě mohla hodit, jsou normálové vektory pro světlo. Když na ně přijde, máme dvě možnosti. V první nalezneme střed každého trojúhelníku, aplikujeme na něj několik výpočtu k získáním tečen k Bezierově křivce na osách x a y, vektorově je vynásobíme a tím získáme vektor kolmý současně k oběma tečnám. Po normalizování ho můžeme použít jako normálu. Druhý způsob je rychlejší a jednodušší, ale méně přesný. Můžeme cheatovat a použít normálový vektor trojúhelníku (spočítaný libovolným způsobem). Tím získáme docela dobrou aproximaci. Osobně preferuji druhou, jednodušší cestu, která ovšem nevypadá tak realistiky.

Ve funkci initBezier() inicializujeme matici kontrolních bodů na výchozí hodnoty. Pohrajte si s nimi, ať vidíte, jak jednoduše se dají měnit tvary povrchů.

void initBezier(void)// Počáteční nastavení kontrolních bodů

{

mybezier.anchors[0][0] = makePoint(-0.75,-0.75,-0.5);

mybezier.anchors[0][1] = makePoint(-0.25,-0.75, 0.0);

mybezier.anchors[0][2] = makePoint( 0.25,-0.75, 0.0);

mybezier.anchors[0][3] = makePoint( 0.75,-0.75,-0.5);

mybezier.anchors[1][0] = makePoint(-0.75,-0.25,-0.75);

mybezier.anchors[1][1] = makePoint(-0.25,-0.25, 0.5);

mybezier.anchors[1][2] = makePoint( 0.25,-0.25, 0.5);

mybezier.anchors[1][3] = makePoint( 0.75,-0.25,-0.75);

mybezier.anchors[2][0] = makePoint(-0.75, 0.25, 0.0);

mybezier.anchors[2][1] = makePoint(-0.25, 0.25,-0.5);

mybezier.anchors[2][2] = makePoint( 0.25, 0.25,-0.5);

mybezier.anchors[2][3] = makePoint( 0.75, 0.25, 0.0);

mybezier.anchors[3][0] = makePoint(-0.75, 0.75,-0.5);

mybezier.anchors[3][1] = makePoint(-0.25, 0.75,-1.0);

mybezier.anchors[3][2] = makePoint( 0.25, 0.75,-1.0);

mybezier.anchors[3][3] = makePoint( 0.75, 0.75,-0.5);

mybezier.dlBPatch = NULL;// Display list ještě neexistuje

}

InitGL() je celkem standardní. Na jejím konci zavoláme funkce pro inicializaci kontrolních bodů, nahrání textury a vygenerování display listu Bezierova povrchu.

int InitGL(GLvoid)// Inicializace

{

glEnable(GL_TEXTURE_2D);// Zapne texturování

glShadeModel(GL_SMOOTH);// Jemné stínování

glClearDepth(1.0f);// Nastavení hloubkového bufferu

glEnable(GL_DEPTH_TEST);// Zapne testování hloubky

glDepthFunc(GL_LEQUAL);// Typ testování hloubky

glClearColor(0.0f, 0.0f, 0.0f, 0.5f);// Černé pozadí

glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST);// Perspektivní korekce

initBezier();// Inicializace kontrolních bodů

LoadGLTexture(&(mybezier.texture), "./data/NeHe.bmp");// Loading textury

mybezier.dlBPatch = genBezier(mybezier, divs);// Generuje display list Bezierova povrchu

return TRUE;// Inicializace v pořádku

}

Vykreslování není oproti minulým tutoriálům vůbec složité. Po všech translacích a rotacích zavoláme display list a potom případně propojíme řídící body červenými čarami. Chcete-li linky zapnout nebo vypnout stiskněte mezerník.

int DrawGLScene(GLvoid)// Všechno kreslení

{

int i, j;// Řídící proměnné cyklů

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);// Smaže obrazovku a hloubkový buffer

glLoadIdentity();// Reset matice

glTranslatef(0.0f, 0.0f, -4.0f);// Přesun do hloubky

glRotatef(-75.0f, 1.0f, 0.0f, 0.0f);// Rotace na ose x

glRotatef(rotz, 0.0f, 0.0f, 1.0f);// Rotace na ose z

glCallList(mybezier.dlBPatch);// Vykreslí display list Bezierova povrchu

if (showCPoints)// Pokud je zapnuté vykreslování mřížky

{

glDisable(GL_TEXTURE_2D);// Vypne texturování

glColor3f(1.0f, 0.0f, 0.0f);// Červená barva

for(i = 0; i < 4; i++)// Horizontální linky

{

glBegin(GL_LINE_STRIP);// Kreslení linek

for(j = 0; j < 4; j++)// Čtyři linky

{

glVertex3d(mybezier.anchors[i][j].x, mybezier.anchors[i][j].y, mybezier.anchors[i][j].z);

}

glEnd();// Konec kreslení

}

for(i = 0; i < 4; i++)// Vertikální linky

{

glBegin(GL_LINE_STRIP);// Kreslení linek

for(j = 0; j < 4; j++)// Čtyři linky

{

glVertex3d(mybezier.anchors[j][i].x, mybezier.anchors[j][i].y, mybezier.anchors[j][i].z);

}

glEnd();// Konec kreslení

}

glColor3f(1.0f, 1.0f, 1.0f);// Bílá barva

glEnable(GL_TEXTURE_2D);// Zapne texturování

}

return TRUE;// V pořádku

}

Práci s Bezierovými křivkami jsme úspěšně dokončili, ale ještě nesmíme zapomenout na fullscreen fix. Odstraňuje problém s přepínám z fullscreenu do okenního módu, kdy některé grafické karty správně neobnovují původní rozlišení obrazovky (např. moje stařičká ATI Rage PRO a několik dalších). Doufám, že budete používat tento pozměněný kód, aby si každý mohl bez komplikací vychutnat vaše skvělá OpenGL dema. V tutoriálu jsme provedli celkem tři změny. První při deklaraci proměnných, kdy jsme vytvořili proměnnou DEVMODE DMsaved. Druhou najdete v CreateGLWindow(), kde jsme tuto pomocnou strukturu naplnili informacemi o aktuálním nastavení. Třetí změna je v KillGLWindow(), kde se obnovuje původní uložené nastavení.

BOOL CreateGLWindow(char* title, int width, int height, int bits, bool fullscreenflag)// Vytváření okna

{

// Deklarace proměnných

EnumDisplaySettings(NULL, ENUM_CURRENT_SETTINGS, &DMsaved);// Uloží aktuální nastavení obrazovky

// Vše ostatní zůstává stejné

}

GLvoid KillGLWindow(GLvoid)// Zavření okna

{

if (fullscreen)// Jsme ve fullscreenu?

{

if (!ChangeDisplaySettings(NULL, CDS_TEST))// Pokud pokusná změna nefunguje

{

ChangeDisplaySettings(NULL, CDS_RESET);// Odstraní hodnoty z registrů

ChangeDisplaySettings(&DMsaved, CDS_RESET);// Použije uložené nastavení

}

else

{

ChangeDisplaySettings(NULL, CDS_RESET);

}

ShowCursor(TRUE);// Zobrazí ukazatel myši

}

// Vše ostatní zůstává stejné

}

Poslední věcí jsou už standardní testy stisku kláves.

// Funkce WinMain()

if (keys[VK_LEFT])// Šipka doleva

{

rotz -= 0.8f;// Rotace doleva

}

if (keys[VK_RIGHT])// Šipka doprava

{

rotz += 0.8f;// Rotace doprava

}

if (keys[VK_UP])// Šipka nahoru

{

divs++;// Menší hranatost povrchu

mybezier.dlBPatch = genBezier(mybezier, divs);// Aktualizace display listu

keys[VK_UP] = FALSE;

}

if (keys[VK_DOWN] && divs > 1)// Šipka dolů

{

divs--;// Větší hranatost povrchu

mybezier.dlBPatch = genBezier(mybezier, divs);// Aktualizace display listu

keys[VK_DOWN] = FALSE;

}

if (keys[VK_SPACE])// Mezerník

{

showCPoints = !showCPoints;// Zobrazí/skryje linky mezi řídícími body

keys[VK_SPACE] = FALSE;

}

Doufám, že pro vás byl tento tutoriál poučný a že od nynějška miluje Bezierovy křivky stejně jako já ;-) Ještě jsem se o tom nezmínil, ale mnohé z vás jistě napadlo, že se s nimi dá vytvořit perfektní morfovací efekt. A velmi jednoduše! Nezapomeňte, se mění poloha pouze šestnácti bodů. Zkuste o tom popřemýšlet...

napsal: David Nikdel <ogapo (zavináč) ithink.net>
přeložil: Michal Turek - Woq <WOQ (zavináč) seznam.cz>

Zdrojové kódy

Visual C++ kód této lekce.
Borland C++ Builder 6 kód této lekce. ( Christian Kindahl )
Code Warrior 5.3 kód této lekce. ( Scott Lupton )
Delphi kód této lekce. ( Joachim Rohde )
Dev C++ kód této lekce. ( Dan )
Euphoria kód této lekce. ( Evan Marshall )
LCC Win32 kód této lekce. ( Robert Wishlaw )
Linux/GLX kód této lekce. ( Rodolphe Suescun )
Mac OS X/Cocoa kód této lekce. ( Bryan Blackburn )
Visual Studio .NET kód této lekce. ( Grant James )

<<< Lekce 27 | Lekce 29 >>>