Lekce 30 - Detekce kolizí
Na podobný tutoriál jste už jistě netrpělivě čekali. Naučíte se základy o detekcích kolizí, jak na ně reagovat a na fyzice založené modelovací efekty (nárazy, působení gravitace ap.). Tutoriál se více zaměřuje na obecnou funkci kolizí než zdrojovým kódům. Nicméně důležité části kódu jsou také popsány. Neočekávejte, že po prvním přečtení úplně všemu z kolizí porozumíte. Je to komplexní námět, se kterým vám pomohu začít.
Zdrojový kód, na němž tato lekce staví, pochází z mého dřívějšího příspěvku do jedné soutěže (najdete na OGLchallenge.dhs.org). Tématem byly Bláznivé kolize a můj příspěvek (mimochodem, získal první místo :-) se jmenoval Magická místnost.
Detekce kolizí jsou obtížné, dodnes nebylo nalezeno žádné snadné řešení. Samozřejmě existují velice obecné algoritmy, které umí pracovat s jakýmkoli druhem objektů, ale očekávejte od nich také patřičnou cenu. My budeme zkoumat postupy, které jsou velmi rychlé, relativně snadné k pochopení a v rámci mezí celkem flexibilní. Důraz musí být vložen nejen na detekci kolize, ale i na reakci objektů na náraz. Je důležité, aby se vše dělo podle fyzikálních zákonů. Máme mnoho věcí na práci! Pojďme se tedy podívat, co všechno se v této lekci naučíme:
Detekce kolizí mezi
- Pohybující se koulí a rovinou
- Pohybující se koulí a válcem
- Dvěma pohybujícími se koulemi
Fyzikálně založené modelování
- Reakce na kolize - odrazy
- Pohyb v gravitaci za použití Eulerových rovnic
Speciální efekty
- Modelování explozí za použití metody Fin-Tree Billboard
- Zvuky pomocí Windows Multimedia Library (pouze Windows)
Zdrojový kód se dělí na pět částí
- Lesson30.cpp - Základní kód tutoriálu
- Image.cpp, Image.h - Nahrávání bitmap
- Tmatrix.cpp, Tmatrix.h - Třída pro práci s maticemi
- Tray.cpp, Tray.h - Třída pro práci s polopřímkami
- Tvector.cpp, Tvector.h - Třída pro práci s vektory
Třídy Vektor, Ray a Matrix jsou velmi užitečné. Dají se použít v jakémkoli projektu. Doporučuji je pečlivě prostudovat, třeba se vám budou někdy hodit.
Detekce kolizí
Polopřímka
Při detekci kolizí využijeme algoritmus, který se většinou používá v trasování polopřímek (ray tracing). Vektorová reprezentace polopřímky je tvořena bodem, který označuje začátek a vektorem (obyčejně normalizovaným) určujícím směr polopřímky. Rovnice polopřímky:
bod_na_polopřímce = začátek + t * směr
Číslo t nabývá hodnot od nuly do nekonečna. Dosadíme-li nulu získáme počáteční bod. U větších čísel dostaneme odpovídající body na polopřímce. Bod, počátek i směr jsou 3D vektory se složkami x, y, a z. Nyní můžeme použít tuto reprezentaci polopřímky k výpočtu průsečíku s rovinou nebo válcem.
Průsečík polopřímky a roviny
Vektorová reprezentace roviny vypadá takto:
Xn dot X = d
Xn je normála roviny, X je bod na jejím povrchu a d je číslo, které určuje vzdálenost roviny od počátku souřadnicového systému.
Překl.: Pod operací "dot" se skrývá skalární součin dvou vektorů (dot product), který se vypočte součtem násobků jednotlivých x, y a z složek. Nechávám ho v původním znění, protože i ve zdrojových kódech budeme volat metodu dot().
Překl.: P dot Q = Px * Qx + Py * Qy + Pz * Qz
Abychom definovali rovinu, potřebujeme 3D bod a vektor, který je kolmý k rovině. Pokud vezmeme za 3D bod vektor (0, 0, 0) a pro normálu vektor (0, 1, 0), protíná rovina osy x a z. Pokud známe bod a normálu, dá se chybějící číslo d snadno dopočítat.
Pozn.: Vektorová reprezentace roviny je ekvivalentní více známé formě Ax + By + Cz + D = 0 (obecná rovnice roviny). Pro přepočet dosaďte za A, B, C složky normály a přiřaďte D = -d.
Nyní máme dvě rovnice
bod_na_polopřímce = začátek + t * směr
Xn dot X = d
Pokud polopřímka protne rovinu v nějakém bodě, musí souřadnice průsečíků vyhovovat oběma rovnicím
Xn dot bod_na_polopřímce = d
Nebo
(Xn dot začátek) + t * (Xn dot směr) = d
Vyjádříme t
t = (d - Xn dot začátek) / (Xn dot směr)
Dosadíme d
t = (Xn dot bod_na_polopřímce - Xn dot začátek) / (Xn dot směr)
Vytkneme Xn
t = (Xn dot (bod_na_polopřímce - začátek)) / (Xn dot směr)
Číslo t reprezentuje vzdálenost od začátku polopřímky k průsečíku s rovinou ve směru polopřímky (ne na kolmici). Dosazením t do rovnice polopřímky získáme kolizní bod. Existuje několik speciálních situací. Pokud Xn dot směr = 0, budou tyto dva vektory navzájem kolmé. Polopřímka prochází rovnoběžně s rovinou a tudíž neexistuje kolizní bod. Pokud je t záporné, průsečík leží před počátečním bodem. Polopřímka nesměřuje k rovině, ale od ní. Opět žádný průsečík.
int TestIntersionPlane(const Plane& plane, const TVector& position, const TVector& direction, double& lamda, TVector& pNormal)
{
double DotProduct = direction.dot(plane._Normal);// Skalární součin vektorů
double l2;// Určuje kolizní bod
if ((DotProduct < ZERO) && (DotProduct > -ZERO))// Je polopřímka rovnoběžná s rovinou?
return 0;// Bez průsečíku
l2 = (plane._Normal.dot(plane._Position - position)) / DotProduct;// Dosazení do vzorce
if (l2 < -ZERO)// Směřuje polopřímka od roviny?
return 0;// Bez průsečíku
pNormal = plane._Normal;// Normála roviny
lamda = l2;// Kolizní bod
return 1;// Průsečík existuje
}
Průsečík polopřímky a válce
Výpočet průsečíku polopřímky s nekonečně dlouhým válcem je mnohem komplikovanější než vysvětlení toho, proč se tím zde nebudeme zabývat. Na pozadí je příliš mnoho matematiky. Mým primárním záměrem je poskytnout a vysvětlit nástroje bez zabíhání do zbytečných detailů, které by stejně někteří nepochopili. Válec je tvořen polopřímkou, která reprezentuje jeho osu, a poloměrem podstavy. Pro detekci kolize se v tomto tutoriálu používá funkce TestIntersetionCylinder(), která vrací jedničku, pokud byl nalezen průsečík, jinak nulu.
int TestIntersionCylinder(const Cylinder& cylinder, const TVector& position, const TVector& direction, double& lamda, TVector& pNormal, TVector& newposition)
V parametrech se předává struktura válce, začátek a směrový vektor polopřímky. Kromě návratové hodnoty získáme z funkce vzdálenost od průsečíku (na polopřímce), normálu vycházející z průsečíku a bod průsečíku.
Kolize mezi dvěma pohybujícími se koulemi
Koule je v geometrii reprezentována středem a poloměrem. Zjištění, jestli do sebe dvě koule narazily je banální. Vypočteme vzdálenost mezi dvěma středy a porovnáme ji se součtem poloměrů. Jak snadné!
Problémy nastanou při hledání kolizního bodu dvou POHYBUJÍCÍCH se koulí. Na obrázku je příklad, kdy se dvě koule přesunou z jednoho místa do druhého za určitý časový úsek. Jejich dráhy se protínají, ale to není dostatečný důvod k tvrzení, že do sebe opravdu narazí. Mohou se například pohybovat rozdílnou rychlostí. Jedna téměř stojí a druhá je za okamžik úplně někde jinde.

V předchozích metodách jsme řešili rovnice dvou geometrických objektů. Pokud podobná rovnice pro daný objekt neexistuje nebo nemůže být použita (pohyb po složité křivce), používá se jiná metoda. V našem případě známe počáteční i koncové body přesunu, časový krok, rychlost (+směr) a metodu zjištění nárazu statických koulí. Rozkouskujeme časový úsek na malé části. Koule budeme v závislosti na nich postupně posunovat a pokaždé testovat kolizi. Pokud najdeme některý bod, kdy je vzdálenost koulí menší než součet jejich poloměrů, vezmeme minulou pozici a označíme ji jako kolizní bod. Může se ještě začít interpolovat mezi těmito dvěma body na rozhraní, kdy kolize ještě nebyla a už je, abychom našli úplně přesnou pozici, ale většinou to není potřeba.
Čím menší bude časový úsek, tím budou části vzniklé rozsekáním menší a metoda bude více přesná (a více náročná na hardware počítače). Například, pokud bude časový úsek 1 a části 3, budeme zjišťovat kolizi v časech 0, 0,33, 0,66 a 1. V následujícím výpisu kódu hledáme koule, které během následujícího časového kroku narazí do kterékoli z ostatních. Funkce vrátí indexy obou koulí, bod a čas nárazu.
int FindBallCol(TVector& point, double& TimePoint, double Time2, int& BallNr1, int& BallNr2)
{
TVector RelativeV;// Relativní rychlost mezi koulemi
TRay rays;// Polopřímka
double MyTime = 0.0;// Hledání přesné pozice nárazu
double Add = Time2 / 150.0;// Rozkouskuje časový úsek na 150 částí
double Timedummy = 10000;// Čas nárazu
TVector posi;// Pozice na polopřímce
// Test všech koulí proti všem ostatním po 150 krocích
for (int i = 0; i < NrOfBalls - 1; i++)// Všechny koule
{
for (int j = i + 1; j < NrOfBalls; j++)// Všechny zbývající koule
{
// Výpočet vzdálenosti
RelativeV = ArrayVel[i] - ArrayVel[j];// Relativní rychlost mezi koulemi
rays = TRay(OldPos[i], TVector::unit(RelativeV));// Polopřímka
if ((rays.dist(OldPos[j])) > 40)// Je vzdálenost větší než 2 poloměry?
{
continue;// Další
}
// Náraz
MyTime = 0.0;// Inicializace před vstupem do cyklu
while (MyTime < Time2)// Přesný bod nárazu
{
MyTime += Add;// Zvětší čas
posi = OldPos[i] + RelativeV * MyTime;//Přesun na další bod (pohyb na polopřímce)
if (posi.dist(OldPos[j]) <= 40)// Náraz
{
point = posi;// Bod nárazu
if (Timedummy > (MyTime - Add))// Bližší náraz, než který jsme už našli (v čase)?
{
Timedummy = MyTime - Add;// Přiřadit čas nárazu
}
BallNr1 = i;// Označení koulí, které narazily
BallNr2 = j;
break;// Ukončí vnitřní cyklus
}
}
}
}
if (Timedummy != 10000)// Našli jsme kolizi?
{
TimePoint = Timedummy;// Čas nárazu
return 1;// Úspěch
}
return 0;// Bez kolize
}
Kolize mezi koulí a rovinou nebo válcem
Nyní už umíme zjistit průsečík polopřímky a roviny/válce. Tyto znalosti použijeme pro hledání kolizí mezi koulí a jedním z těchto objektů. Potřebujeme najít přesný bod nárazu. Převod znalostí z polopřímky na pohybující se kouli je relativně snadný. Podívejte se na levý obrázek, možná, že podstatu pochopíte sami.
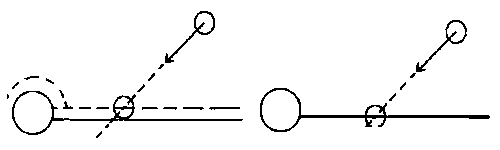
Každá koule sice má poloměr, ale my ji budeme brát jako bezrozměrnou části, která má pouze pozici. K povrchu tělesa přičteme ve směru normálového vektoru offset určený poloměrem koule. Neboli k poloměru válce přičteme průměr koule (2 poloměry; z každé strany jeden). Operací jsme se vrátili k detekci kolize polopřímka - válec. Rovina je ještě jednodušší. Posuneme ji směrem ke kouli o její poloměr. Na obrázku jsou čárkovaně nakresleny "virtuální" objekty pro testy kolizí a plně objekty, které program vykreslí. Kdybychom k objektům při testech nepřipočítávali offset, koule by před odrazem z poloviny pronikaly do objektů (obrázek vpravo).
Máme-li určit místo nárazu, je vhodné nejdříve zjistit, jestli kolize nastane při aktuálním časovém úseku. Protože polopřímka má nekonečnou délku, je vždy možné, že se kolizní bod nachází až někde za novou pozicí koule. Abychom to zjistili, spočítáme novou pozici a určíme vzdálenost mezi počátečním a koncovým bodem. Pokud je tato vzdálenost kratší než vzdálenost, o kterou se objekt posune, tak máme jistotu, že kolize nastane v tomto časovém úseku. Abychom spočítali přesný čas kolize použijeme následující jednoduchou rovnici. Dst představuje vzdálenost mezi počátečním a koncovým bodem, Dsc vzdálenost mezi počátečním a kolizním bodem a časový krok je definován jako T. Řešením získáme čas kolize Tc.
Tc = Dsc * T / Dst
Výpočet se provede samozřejmě jenom tehdy, když má kolize nastat v tomto časovém kroku. Vrácený čas je zlomkem (částí) celého časového kroku. Pokud bude časový krok 1 s a my nalezneme kolizní bod přesně uprostřed vzdálenosti, čas kolize se bude rovnat 0,5 s. Je interpretován jako: V časovém okamžiku 0,5 sekund po začátku přesunu do sebe objekty narazí. Kolizní bod se vypočte násobením času Tc aktuální rychlostí a přičtením počátečního bodu.
bod_kolize = start + rychlost * Tc
Tento kolizní bod je však na objektu s offsetem (pomocném). Abychom nalezli bod nárazu na reálném objektu, přičteme k bodu kolize invertovaný normálový vektor z bodu kolize, který má velikost poloměru koule. Normálový vektor získáme z funkce pro kolize. Všimněte si, že funkce pro kolizi s válcem vrací bod nárazu, takže nemusí být znovu počítán.
Modelování založené na fyzice
Reakce na náraz
Ošetření toho, jak se koule zachová po nárazu je stejně důležité jako samotné nalezení kolizního bodu. Použité algoritmy a funkce popisují přesný bod nárazu, normálový vektor vycházející z objektů v místě nárazu a časový úsek, ve kterém kolize nastala.
Při odrazech nám pomohou fyzikální zákony. Implementujeme poučku: "Úhel dopadu se rovná úhlu odrazu". Oba úhly se vztahují k normálovému vektoru, který vychází z objektu v kolizním bodě. Následující obrázek ukazuje odraz polopřímky od koule.

I je směrový vektor před nárazem, N je normálový vektor v bodě kolize a R je směrový vektor po odrazu, který se vypočte podle následující rovnice:
R = 2 * (-I dot N) * N + I
Omezení spočívá v tom, že I i N musí být jednotkové vektory. U nás však délka vektoru reprezentuje rychlost a směr koule, a proto nemůže být bez transformace dosazen do rovnice. Potřebujeme z něj vyjmout rychlost. Nalezneme jeho velikost a vydělíme jí jednotlivé x, y, z složky. Získaný jednotkový vektor dosadíme do rovnice a vypočteme R. Jsme skoro u konce. Vektor nyní míří ve směru odražené polopřímky, ale nemá původní délku. Minule jsme dělili, takže teď budeme násobit.
Následující výpis kódu se používá pro výpočet odrazu po kolizi koule s rovinou nebo válcem. Uvedený algoritmus pracuje i s jinými povrchy, nezáleží na jejich tvaru. Pokud nalezneme bod kolize a normálu, je odraz vždy stejný.
rt2 = ArrayVel[BallNr].mag();// Uloží délku vektoru
ArrayVel[BallNr].unit();// Normalizace vektoru
// Výpočet odrazu
ArrayVel[BallNr] = TVector::unit((normal * (2 * normal.dot(-ArrayVel[BallNr]))) + ArrayVel[BallNr]);
ArrayVel[BallNr] = ArrayVel[BallNr] * rt2;// Nastavení původní délky
Když se koule srazí s jinou
Ošetření vzájemného nárazu dvou pohybujících se koulí je mnohem obtížnější. Musí být vyřešeny složité rovnice. Nebudeme nic odvozovat, pouze vysvětlím výsledek. Situace při kolizi dvou koulí vypadá přibližně takto:
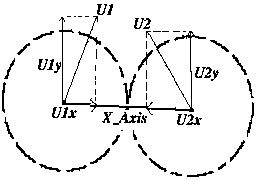
Vektory U1 a U2 představují rychlost koulí v čase nárazu. Středy dohromady spojuje osa X_Axis, na které leží vektory U1x a U2x, což jsou vlastně průměty rychlosti. U1y a U2y jsou projekce rychlosti na osu, která je kolmá k X_Axis. K jejich výpočtu postačí jednoduchý skalární součin.
Do následujících rovnic dosazujeme ještě čísla M1 a M2, která vyjadřují hmotnost koulí. Snažíme se vypočítat orientaci vektorů rychlosti U1 a U2 po odrazu. Budou je vyjadřovat nové vektory V1 a V2. Čísla V1x, V1y, V2x, V2y jsou opět průměty.
a) najít X_Axis
X_Axis = (střed2 - střed1)
Jednotkový vektor, X_Axis.unit();
b) najít projekce
U1x = X_Axis * (X_Axis dot U1)
U1y = U1 - U1x
U2x = -X_Axis * (-X_Axis dot U2)
U2y = U2 - U2x
c) najít nové rychlosti
V1x = ((U1x * M1) + (U2x * M2) - (U1x - U2x) * M2) / (M1 + M2)
V2x = ((U1x * M1) + (U2x * M2) - (U2x - U1x) * M1) / (M1 + M2)
V naší aplikaci nastavujeme jednotkovou hmotnost (M1 = M2 = 1), a proto se výpočet výsledných vektorů velmi zjednoduší.
d) najít konečné rychlosti
V1y = U1y
V2y = U2y
V1 = V1x + V1y
V2 = V2x + V2y
Odvození rovnic stálo hodně práce, ale jakmile se nacházejí v této formě, je jejich použití docela snadné. Kód, které vykonává srážky dvou koulí vypadá takto:
TVector pb1, pb2, xaxis, U1x, U1y, U2x, U2y, V1x, V1y, V2x, V2y;// Deklarace proměnných
double a, b;
pb1 = OldPos[BallColNr1] + ArrayVel[BallColNr1] * BallTime;// Nalezení pozice koule 1
pb2 = OldPos[BallColNr2] + ArrayVel[BallColNr2] * BallTime;// Nalezení pozice koule 2
xaxis = (pb2 - pb1).unit();// Nalezení X_Axis
a = xaxis.dot(ArrayVel[BallColNr1]);// Nalezení projekce
U1x = xaxis * a;// Nalezení průmětů vektorů
U1y = ArrayVel[BallColNr1] - U1x;
xaxis = (pb1 - pb2).unit();
b = xaxis.dot(ArrayVel[BallColNr2]);// To samé pro druhou kouli
U2x = xaxis * b;
U2y = ArrayVel[BallColNr2] - U2x;
V1x = (U1x + U2x - (U1x - U2x)) * 0.5;// Nalezení nových rychlostí
V2x = (U1x + U2x - (U2x - U1x)) * 0.5;
V1y = U1y;
V2y = U2y;
for (j = 0; j < NrOfBalls; j++)// Posun všech koulí do času nárazu
{
ArrayPos[j] = OldPos[j] + ArrayVel[j] * BallTime;
}
ArrayVel[BallColNr1] = V1x + V1y;// Nastavení právě vypočítaných vektorů koulím, které do sebe narazily
ArrayVel[BallColNr2] = V2x + V2y;
Pohyb v gravitaci za použití Eulerových rovnic
Pro simulaci realistických pohybů nejsou nárazy, hledání kolizních bodů a odrazy dostatečné. Musí být přidán ještě pohyb podle fyzikálních zákonů. Asi nejpoužívanější metodou jsou Eulerovy rovnice. Všechny výpočty se vykonávají pro určitý časový úsek. To znamená, že se celá simulace neposouvá vpřed plynule, ale po určitých skocích. Představte si, že máte fotoaparát a každou vteřinu výslednou scénu vyfotíte. Během této vteřiny se provedou všechny pohyby, testy kolizí a odrazy. Výsledný obrázek se zobrazí na monitoru a zůstane tam až do další vteřiny. Opět stejné výpočty a další zobrazení. Takto pracují všechny počítačové animace, ale mnohem rychleji. Oko, stejně jako u filmu, vidí plynulý pohyb. V závislosti na Eulerových rovnicích se rychlost a pozice v každém časovém kroku změní takto:
nová_rychlost = stará_rychlost + zrychlení * časový úsek
nová_pozice = stará_pozice + nová_rychlost * časový úsek
Nyní se objekty pohybují a testují na kolize s použitím nové rychlosti. Zrychlení objektu je získáno vydělením síly, která na něj působí, jeho hmotností.
zrychlení = síla / hmotnost
V tomto demu je gravitace jediná síla, která působí na objekt. Může být reprezentována vektorem, který udává gravitační zrychlení. U nás se bude tento vektor rovnat (0; -0,5; 0). To znamená, že na začátku každého časového úseku spočítáme novou rychlost koule a s testováním kolizí ji posuneme. Pokud během časového úseku narazí (např. po 0,5 s), posuneme ji na pozici kolize, vypočteme odraz (nový vektor rychlosti) a přesuneme ji o zbývající čas (0,5 s). V něm opět testujeme kolize atd. Opakujeme tak dlouho, dokud zbývá nějaký čas.
Pokud je přítomno více pohybujících se objektů, musí být nejprve testován každý z nich na nárazy do statických objektů. Uloží se časově nejbližší z nich. Potom se provedou testy nárazů mezi pohybujícími se objekty - každý s každým. Vrácený čas je porovnán s časem u testů se statickými objekty a v úvahu je brán nejbližší náraz. Celá simulace se posune do tohoto času. Vypočte se odraz objektu a opět se provedou detekce nárazů do statických objektů atd. atd. atd. - dokud zbývá nějaký čas. Překreslí se scéna a vše se opakuje nanovo.
Speciální efekty
Exploze
Kdykoli, když se objekty srazí, nastane exploze, která se zobrazí na souřadnicích průsečíku. Velmi jednoduchou cestou je alfablending dvou polygonů, které jsou navzájem kolmé a jejich střed je na souřadnicích kolizního bodu. Oba polygony se postupně zvětšují a zprůhledňují. Alfa hodnota se zmenšuje z počáteční jedničky až na nulu. Díky Z bufferu může spousta alfablendovaných polygonů způsobovat problémy - navzájem se překrývají, a proto si půjčíme techniku používanou při renderingu částic. Abychom vše dělali správně, musíme polygony řadit od zadních po přední podle vzdálenosti od pozorovatele. Také vypneme zápis do Depth bufferu (ne čtení). Všimněte si, že omezujeme počet explozí na maximálně dvacet na jeden snímek. Nastane-li jich najednou více, pole se zaplní a další se nebudou brát v úvahu. Následuje kód, který aktualizuje a renderuje exploze.
glEnable(GL_BLEND);// Blending
glDepthMask(GL_FALSE);// Vypne zápis do depth bufferu
glBindTexture(GL_TEXTURE_2D, texture[1]);// Textura exploze
for(i = 0; i < 20; i++)// Prochází výbuchy
{
if(ExplosionArray[i]._Alpha >= 0)// Je exploze vidět?
{
glPushMatrix();// Záloha matice
ExplosionArray[i]._Alpha -= 0.01f;// Aktualizace alfa hodnoty
ExplosionArray[i]._Scale += 0.03f;// Aktualizace měřítka
glColor4f(1, 1, 0, ExplosionArray[i]._Alpha);// Žlutá barva s průhledností
glScalef(ExplosionArray[i]._Scale, ExplosionArray[i]._Scale, ExplosionArray[i]._Scale);// Změna měřítka
glTranslatef((float)ExplosionArray[i]._Position.X() / ExplosionArray[i]._Scale, (float)ExplosionArray[i]._Position.Y() / explosionArray[i]._Scale, (float)ExplosionArray[i]._Position.Z() / ExplosionArray[i]._Scale);// Přesun na pozici kolizního bodu, měřítko je offsetem
glCallList(dlist);// Zavolá display list
glPopMatrix();// Obnova původní matice
}
}
glDepthMask(GL_TRUE);// Obnova původních parametrů OpenGL
glDisable(GL_BLEND);
glDisable(GL_TEXTURE_2D);
Zvuky
Pro přehrávání zvuků se používá funkce PlaySound() z multimediální knihovny Windows - rychlá cesta, jak bez problémů přehrát .wav zvuk.
Vysvětlení kódu
Gratuluji... pokud stále čtete, úspěšně jste se prokousali dlouhou a náročnou teoretickou sekcí. Předtím, než si začnete hrát s demem, měl by být ještě vysvětlen zdrojový kód. Ze všeho nejdříve se ale půjdeme podívat na globální proměnné.
Vektory dir a pos reprezentují pozici a směr kamery, kterou v programu pohybujeme funkcí gluLookAt(). Pokud scéna není vykreslována v módu "sledování koule", otáčí se kolem osy y.
TVector dir;// Směr kamery
TVector pos(0, -50, 1000);// Pozice kamery
float camera_rotation = 0;// Rotace scény na ose y
Gravitace, která působí na koule.
TVector accel(0, -0.05, 0);// Gravitační zrychlení aplikované na koule
Pole, která ukládají novou a starou pozici všech koulí a jejich směr. Počet koulí je natvrdo nastaven na deset.
TVector ArrayVel[10];// Rychlost koulí
TVector ArrayPos[10];// Pozice koulí
TVector OldPos[10];// Staré pozice koulí
Časový úsek pro simulaci.
double Time = 0.6;// Časový krok simulace
Pokud je tato proměnná v jedničce, změní se mód kamery tak, aby sledovala pohyby koule. Pro její umístění a nasměrování se použije pozice a směr koule s indexem 1, která tedy bude vždy v záběru.
int hook_toball1 = 0;// Sledovat kamerou kouli?
Následující struktury se popisují samy svým jménem. Budou ukládat data o rovinách, válcích a explozích.
struct Plane// Struktura roviny
{
TVector _Position;
TVector _Normal;
};
struct Cylinder// Struktura válce
{
TVector _Position;
TVector _Axis;
double _Radius;
};
struct Explosion// Struktura exploze
{
TVector _Position;
float _Alpha;
float _Scale;
};
Objekty struktur.
Plane pl1, pl2, pl3, pl4, pl5;// Pět rovin místnosti (bez stropu)
Cylinder cyl1, cyl2, cyl3;// Tři válce
Explosion ExplosionArray[20];// Dvacet explozí
Textury, display list, quadratic.
GLuint texture[4];// Čtyři textury
GLuint dlist;// Display list výbuchu
GLUquadricObj *cylinder_obj;// Quadratic pro kreslení koulí a válců
Funkce pro kolize koulí se statickými objekty a mezi koulemi navzájem.
int TestIntersionPlane(const Plane& plane, const TVector& position, const TVector& direction, double& lamda, TVector& pNormal);
int TestIntersionCylinder(const Cylinder& cylinder, const TVector& position, const TVector& direction, double& lamda, TVector& pNormal, TVector& newposition);
int FindBallCol(TVector& point, double& TimePoint, double Time2, int& BallNr1, int& BallNr2);
Loading textur, inicializace proměnných, logika simulace, renderování scény a inicializace OpenGL.
void LoadGLTextures();
void InitVars();
void idle();
int DrawGLScene(GLvoid);
int InitGL(GLvoid)
Pro informace o geometrických třídách vektoru, polopřímky a matice nahlédněte do zdrojových kódů. Jsou velmi užitečné a mohou být bez problémů využity ve vašich vlastních programech.
Nejdůležitější kroky simulace nejprve popíši pseudokódem.
while (časový úsek != 0)
{
for (každá koule)
{
Výpočet nejbližší kolize s rovinami;
Výpočet nejbližší kolize s válci;
Uložit/nahradit "záznam" o kolizi, pokud je to do teď nejbližší kolize v čase;
}
Testy kolizí mezi pohybujícími se koulemi;
Uložit/nahradit "záznam" o kolizi, pokud je to do teď nejbližší kolize v čase;
if (nastala kolize?)
{
Přesun všech koulí do času nejbližší kolize;
(Už máme vypočten bod, normálu a čas kolize.)
Výpočet odrazu;
časový úsek -= čas kolize;
}
else
{
Přesun všech koulí na konec časového úseku;
}
}
Zdrojový kód založený na pseudokódu je na první pohled mnohem více náročný na čtení a hlavně pochopení, nicméně v základu je jeho přesnou implementací.
void idle()// Simulační logika - kolize
{
// Deklarace proměnných
double rt, rt2, rt4, lamda = 10000;
TVector norm, uveloc;
TVector normal, point, time;
double RestTime, BallTime;
TVector Pos2;
int BallNr = 0, dummy = 0, BallColNr1, BallColNr2;
TVector Nc;
if (!hook_toball1)// Pokud kamera nesleduje kouli
{
camera_rotation += 0.1f;// Pootočení scény
if (camera_rotation > 360)// Ošetření přetečení
{
camera_rotation = 0;
}
}
RestTime = Time;
lamda = 1000;
// Výpočet rychlostí všech koulí pro následující časový úsek (Eulerovy rovnice)
for (int j = 0; j < NrOfBalls; j++)
{
ArrayVel[j] += accel * RestTime;
}
while (RestTime > ZERO)// Dokud neskončil časový úsek
{
lamda = 10000;// Inicializace na velmi vysokou hodnotu
// Kolize všech koulí s rovinami a válci
for (int i = 0; i < NrOfBalls; i++)// Všechny koule
{
// Výpočet nové pozice a vzdálenosti
OldPos[i] = ArrayPos[i];
TVector::unit(ArrayVel[i], uveloc);
ArrayPos[i] = ArrayPos[i] + ArrayVel[i] * RestTime;
rt2 = OldPos[i].dist(ArrayPos[i]);
// Kolize koule s rovinou
if (TestIntersionPlane(pl1, OldPos[i], uveloc, rt, norm))
{
// Čas nárazu
rt4 = rt * RestTime / rt2;
// Pokud je menší než některý z dříve nalezených nahradit ho
if (rt4 <= lamda)
{
if (rt4 <= RestTime + ZERO)
{
if (!((rt <= ZERO) && (uveloc.dot(norm) > ZERO)))
{
normal = norm;
point = OldPos[i] + uveloc * rt;
lamda = rt4;
BallNr = i;
}
}
}
}
if (TestIntersionPlane(pl2, OldPos[i], uveloc, rt, norm))
{
// To samé jako minule, ale s jinou rovinou
}
if (TestIntersionPlane(pl3, OldPos[i], uveloc, rt, norm))
{
// To samé jako minule, ale s jinou rovinou
}
if (TestIntersionPlane(pl4, OldPos[i], uveloc, rt, norm))
{
// To samé jako minule, ale s jinou rovinou
}
if (TestIntersionPlane(pl5, OldPos[i], uveloc, rt, norm))
{
// To samé jako minule, ale s jinou rovinou
}
// Kolize koule s válcem
if (TestIntersionCylinder(cyl1, OldPos[i], uveloc, rt, norm, Nc))
{
rt4 = rt * RestTime / rt2;
if (rt4 <= lamda)
{
if (rt4 <= RestTime + ZERO)
{
if (!((rt <= ZERO) && (uveloc.dot(norm) > ZERO)))
{
normal = norm;
point = Nc;
lamda = rt4;
BallNr = i;
}
}
}
}
if (TestIntersionCylinder(cyl2, OldPos[i], uveloc, rt, norm, Nc))
{
// To samé jako minule, ale s jiným válcem
}
if (TestIntersionCylinder(cyl3, OldPos[i], uveloc, rt, norm, Nc))
{
// To samé jako minule, ale s jiným válcem
}
}
// Kolize mezi koulemi
if (FindBallCol(Pos2, BallTime, RestTime, BallColNr1, BallColNr2))
{
if (sounds)// Jsou zapnuté zvuky?
{
PlaySound("Data/Explode.wav", NULL, SND_FILENAME | SND_ASYNC);
}
if ((lamda == 10000) || (lamda > BallTime))
{
RestTime = RestTime - BallTime;
TVector pb1, pb2, xaxis, U1x, U1y, U2x, U2y, V1x, V1y, V2x, V2y;// Deklarace proměnných
double a, b;
pb1 = OldPos[BallColNr1] + ArrayVel[BallColNr1] * BallTime;// Nalezení pozice koule 1
pb2 = OldPos[BallColNr2] + ArrayVel[BallColNr2] * BallTime;// Nalezení pozice koule 2
xaxis = (pb2 - pb1).unit();// Nalezení X_Axis
a = xaxis.dot(ArrayVel[BallColNr1]);// Nalezení projekce
U1x = xaxis * a;// Nalezení průmětů vektorů
U1y = ArrayVel[BallColNr1] - U1x;
xaxis = (pb1 - pb2).unit();
b = xaxis.dot(ArrayVel[BallColNr2]);// To samé pro druhou kouli
U2x = xaxis * b;
U2y = ArrayVel[BallColNr2] - U2x;
V1x = (U1x + U2x - (U1x - U2x)) * 0.5;// Nalezení nových rychlostí
V2x = (U1x + U2x - (U2x - U1x)) * 0.5;
V1y = U1y;
V2y = U2y;
for (j = 0; j < NrOfBalls; j++)// Aktualizace pozic všech koulí
{
ArrayPos[j] = OldPos[j] + ArrayVel[j] * BallTime;
}
ArrayVel[BallColNr1] = V1x + V1y;// Nastavení právě vypočítaných vektorů koulím, které do sebe narazily
ArrayVel[BallColNr2] = V2x + V2y;
// Aktualizace pole explozí
for(j = 0; j < 20; j++)// Všechny exploze
{
if (ExplosionArray[j]._Alpha <= 0)// Hledá volné místo
{
ExplosionArray[j]._Alpha = 1;// Neprůhledná
ExplosionArray[j]._Position = ArrayPos[BallColNr1];// Pozice
ExplosionArray[j]._Scale = 1;// Měřítko
break;// Ukončit prohledávání
}
}
continue;// Opakovat cyklus
}
}
// Konec testů kolizí
// Pokud se prošel celý časový úsek a byly vypočteny reakce koulí, které narazily
if (lamda != 10000)
{
RestTime -= lamda;// Odečtení času kolize od časového úseku
for (j = 0; j < NrOfBalls; j++)
{
ArrayPos[j] = OldPos[j] + ArrayVel[j] * lamda;
}
rt2 = ArrayVel[BallNr].mag();
ArrayVel[BallNr].unit();
ArrayVel[BallNr] = TVector::unit((normal * (2 * normal.dot(-ArrayVel[BallNr]))) + ArrayVel[BallNr]);
ArrayVel[BallNr] = ArrayVel[BallNr] * rt2;
// Aktualizace pole explozí
for(j = 0; j < 20; j++)// Všechny exploze
{
if (ExplosionArray[j]._Alpha <= 0)// Hledá volné místo
{
ExplosionArray[j]._Alpha = 1;// Neprůhledná
ExplosionArray[j]._Position = ArrayPos[BallColNr1];// Pozice
ExplosionArray[j]._Scale = 1;// Měřítko
break;// Ukončit prohledávání
}
}
}
else
{
RestTime = 0;// Ukončení hlavního cyklu a vlastně i funkce
}
}
}
Jak jsem už napsal na začátku, předmět kolizí je velmi těžký a rozsáhlý, aby se dal popsat jen v jednom tutoriálu, přesto jste se naučili spoustu nových věcí. Můžete začít vytvářet vlastní působivá dema. Nyní, když chápete základy, budete lépe rozumět i cizím zdrojovým kódům, které vás zase posunou o kousek dál. Přeji hodně štěstí.
napsal: Dimitrios Christopoulos
přeložil: Michal Turek - Woq <WOQ (zavináč) seznam.cz>
Informace o autorovi
V současné době pracuje jako softwarový inženýr virtuální reality Helénského světa v Aténách/Řecko (www.fhw.gr). Ačkoli se narodil v Německu, studoval řeckou univerzitu Patras na bakaláře přírodních věd v počítačovém inženýrství a informatice. Je také držitelem MSc degree (titul Magistra přírodních věd) z univerzity Hull (Anglie) v počítačové grafice a virtuálním prostředí.
První krůčky s programováním podnikl v jazyce Basic na Commodoru 64. Po začátku studia se přeorientoval na C/C++/Assembler na platformě PC. Během několika minulých let si jako grafické API zvolil OpenGL.
Zdrojové kódy
- Visual C++ kód této lekce.
- Borland C++ Builder 6 kód této lekce. ( Christian Kindahl )
- Code Warrior 5.3 kód této lekce. ( Scott Lupton )
- Delphi kód této lekce. ( Felix Hahn )
- Dev C++ kód této lekce. ( Conrado )
- JoGL kód této lekce. ( Abdul Bezrati )
- Linux/GLX kód této lekce. ( Rodolphe Suescun )
- Mac OS X/Cocoa kód této lekce. ( Bryan Blackburn )
- Visual Studio .NET kód této lekce. ( Grant James )